Interpreting the P value when Prism fits both slope and intercept
Prism reports the P value testing the null hypothesis that the overall slope is zero. The P value answers this question:
If there were no linear relationship between X and Y overall, what is the probability that randomly selected points would result in a regression line as far from horizontal (or further) than you observed?
Equivalently:
If there were no linear relationship between X and Y overall, what is the probability that randomly selected points would result in an R2 value as high (or further) as you observed?
The P value is calculated from an F test, and Prism also reports the value of F and its degrees of freedom. You would get exactly the same P value from the t ratio computed by dividing the slope by its standard error.
Interpreting the P value when Prism fits only the slope
Beware of the P value from linear regression when you force the line to go through the origin or some other point. It is easy to misinterpret. The graph below demonstrates the problem:
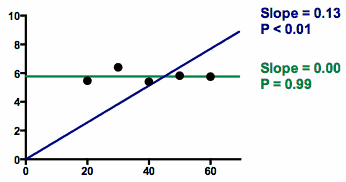
The data points almost form a horizontal line.
When fit with linear regression the usual way (fit both slope and intercept; green line), the best fit value of the slope is 0.00. The P value answers the question: If the true slope is zero, what is the chance that the slope will be further from zero than the observed slope due only to random sampling. Since the observed slope is zero, there is almost a 100% chance of obtaining a slope that is further than zero than observed! So the P value is greater than 0.99, as high as a P value can be. Some people are confused and think the P value should be small purely because the points for a pattern. Not so. The P value, from conventional linear regression fitting both slope and intercept, will be small only when the points form a linear pattern that is not horizontal.
The results are very different when you fit linear regression with the constraint that the line has to go through the origin (blue line). To make the line go through the origin and also go near the points, the best-fit line has a slope is far from zero. Since the line is far from horizontal, the P value is tiny. Given the constraint that the line must go through the origin (X=0, Y=0; lower-left of graph), the data are quite convincing that best fit line is far from horizontal, so it makes sense that the P value is tiny.
Constraining a line to go through the origin (or some other point) can be very useful in some situations. Usually this option is used to fit calibration curves used for interpolation, in which case the P value is not useful. If you force the line through the origin, be very wary when interpreting the P value. It is rarely useful, and easy to misinterpret.