Prism offers a choice of three algorithms for controlling the FDR. The three algorithms all work in a similar manner.
1.Calculate a P value for each comparison.
2.Rank the P values from low to high.
3. Start with the largest P value.
4.Compute a threshold for the largest P value. That threshold value depends on the number of P values being looked at. For the method of Benjamini, Krieger and Yekutieli, the threshold also depends on the estimate of the number of true null hypotheses provided by the method.
5. If the P value is less than the threshold, then all P values are flagged as discoveries, and you are done. Otherwise, continue.
6.Go to the second largest P value.
7.Compute a threshold for the second highest P value. This threshold will be smaller than the threshold for the largest P value. Computing the threshold (see below) depends on the rank of the P value, the number of P values and (for the method of Benjamini, Krieger and Yekutieli) the estimate of the number of true null hypotheses (computed by the method; nothing for you to think about).
8. If the P value is less than the threshold, that P value and all smaller ones are flagged as discoveries and you are done. Otherwise continue.
9.Go to the next P lower value.
10.Compute a threshold for this rank. It will be smaller than the previous threshold.
11. If the P value is less than the threshold, that P value and all smaller ones are flagged as discoveries and you are done. Otherwise repeat steps 9-10 until done.
The difference between the three methods is how they compute the threshold values. The table below gives the details, where Q is the desired false discovery rate (as a percentage), N is the number of P values in the set, and Ntrue is the number of the null hypotheses estimated to be true (part of the second method below). Define q to equal Q/100. This converts the value you enter as a percentage into a fraction.
Method |
Threshold for smallest P value |
Threshold for largest P value |
Original method of Benjamini and Hochberg (1) |
q/n |
q |
Two-stage step-up method of Benjamini, Krieger and Yekutieli (2) |
q/[(1+q)Ntrue] |
[q/(1+q)] * (N / Ntrue) |
Corrected method of Benjamini & Yekutieli (3) |
q/[N* (1 + 1/2 + 1/3 + ... + 1/N)] |
q /(1 + 1/2 + 1/3 + ... + 1/N) |
Notes:
•The variable q is defined to be Q/100, where Q is the desired false discovery rate (as a percentage) you enter.
•The thresholds for the P values between the smallest and largest are determined by a linear interpolation between those extremes.
•The threshold is computed as a fraction (not a percentage), to compare to a P value.
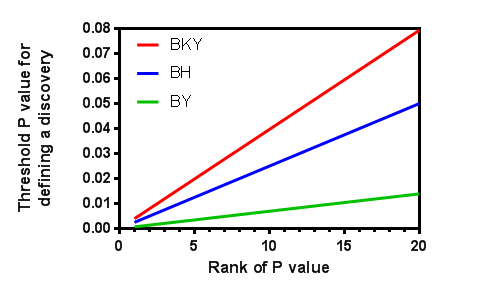
Here is a graph showing the thresholds for analyzing 20 P values (N=20), you set Q=5% and Ntrue=12 (computed by the BKY method from the data, and only applicable for the red line). You can see that the two-stage linear step-up method method of Benjamini, Krieger and Yekuteili (red) has largest thresholds so has the most power, and the corrected method of Benjamini & Yekutieli (green) has the least power. You can also see that the methods diverge the most when computing the threshold for the largest P values and nearly converge for smaller P values.
References
1.Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 289–300 (1995).
2.Benjamini, Y., Krieger, A. M. & Yekutieli, D. Adaptive linear step-up procedures that control the false discovery rate. Biometrika 93, 491–507 (2006). We use the method defined in section 6 of this paper, the two-stage linear step-up procedure.
3.Benjamini, Y., & Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. Annals of statistics, 1165–1188.