Assumptions of the analysis

Spherical clusters

K-means clustering assumes that the clusters are spherical in shape. This means that clusters with different geometric shapes may not be accurately detected or identified by K-means clustering.

Equal variance of clusters

This assumption indicates that K-means assumes that the distribution of data around each cluster center is roughly equal. The result of this assumption is that K-means may “miss” clusters that have less dense arrangement of data points if other clusters contain tightly grouped data points.

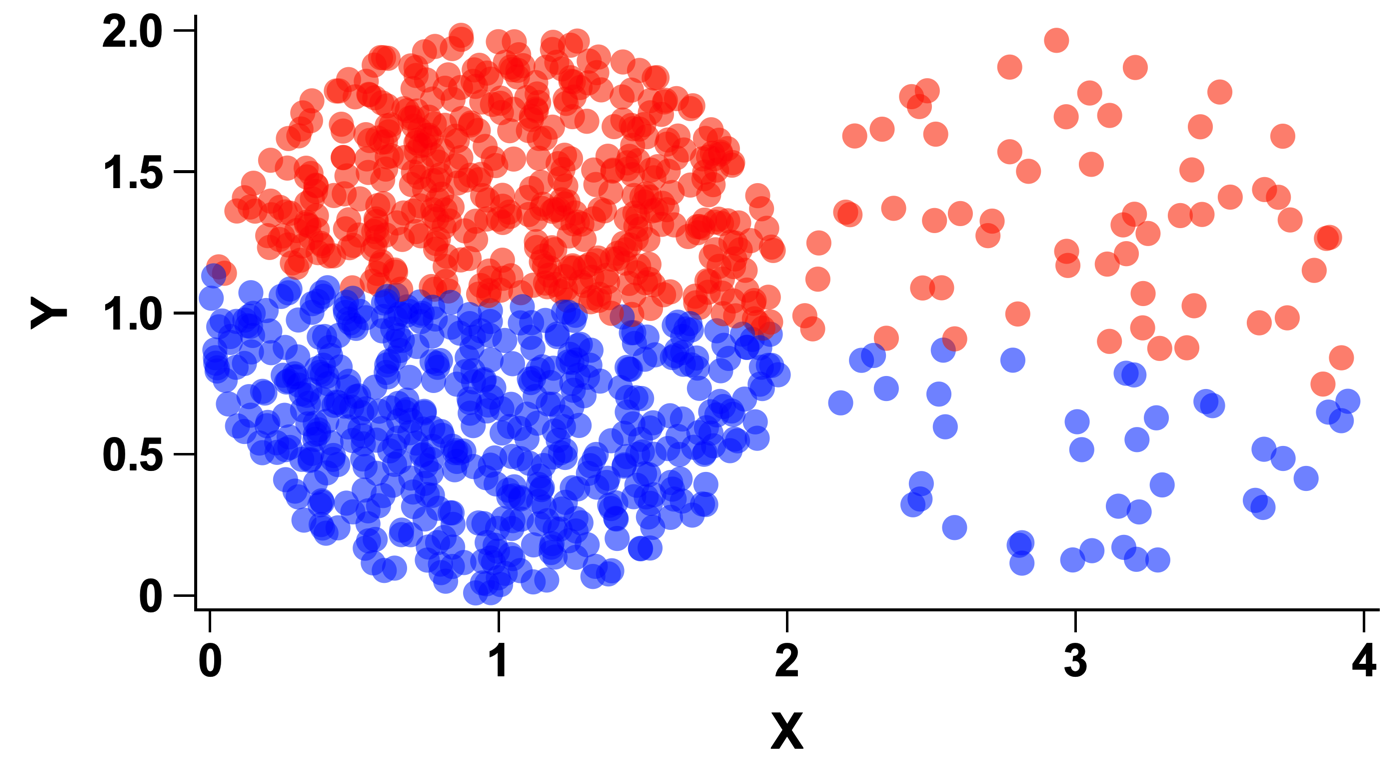
Equal cluster sizes

The analysis assumes that each cluster contains roughly the same number of data points. When this assumption is violated, K-means clustering may fail to identify clusters that would otherwise seem reasonably obvious. The image below shows an example of this, where one cluster contains 10x as many data points as the other. K-means was performed with k=2. Because of the assumption that each cluster should have the same number of observations, you can see that the K-means algorithm identifies clusters that may not seem logical otherwise.

Independent variables

There are a variety of reasons why this assumption is important when performing K-means clustering analysis. One reason is that if variables are highly correlated (not independent), then the determined location of cluster centers may be skewed, with more “weight” applied in the direction of the correlated variables. Additionally, as mentioned above, this analysis assumes that the clusters are spherical in the multi-dimensional space. When multiple variables are correlated, the shape of the clusters in the data may be more elliptical in reality. However, because K-means assumes spherical clusters, the clustering results may be poor under these conditions.