What can an outlier tests do?

No mathematical calculation can tell you for sure whether the outlier came from the same, or a different, population than the others. Statistical calculations, however, can answer this question:

If the values really were all sampled from a Gaussian distribution, what is the chance that you would find one value as far from the others as you observed?

If this probability is small, then you will conclude that the outlier is not from the same distribution as the other values. Assuming you answered no to all three questions above, you have justification to exclude it from your analysis.

Statisticians have devised several methods for detecting outliers. All the methods first quantify how far the outlier is from the other values. This can be the difference between the outlier and the mean of all points, the difference between the outlier and the mean of the remaining values, or the difference between the outlier and the next closest value. Next, standardize this value by dividing by some measure of scatter, such as the SD of all values, the SD of the remaining values, or the range of the data. Finally, compute a P value answering this question: If all the values were really sampled from a Gaussian population, what is the chance of randomly obtaining an outlier so far from the other values? If the P value is small, you conclude that the deviation of the outlier from the other values is statistically significant, and most likely from a different population.

How Grubbs's test works

Grubbs' test is one of the most popular ways to define outliers, and is quite easy to understand. This method is also called the ESD method (extreme studentized deviate).

The first step is to quantify how far the outlier is from the others. Calculate the ratio Z as the difference between the outlier and the mean divided by the SD. If Z is large, the value is far from the others. Note that you calculate the mean and SD from all values, including the outlier.

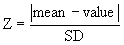
You'll sometimes see this value referred to as G instead of Z.

Since 5% of the values in a Gaussian population are more than 1.96 standard deviations from the mean, your first thought might be to conclude that the outlier comes from a different population if Z is greater than 1.96. This approach only works if you know the population mean and SD from other data. Although this is rarely the case in experimental science, it is often the case in quality control. You know the overall mean and SD from historical data, and want to know whether the latest value matches the others. This is the basis for quality control charts.

When analyzing experimental data, you don't know the SD of the population. Instead, you calculate the SD from the data. The presence of an outlier increases the calculated SD. Since the presence of an outlier increases both the numerator (difference between the value and the mean) and denominator (SD of all values), Z can not get as large as you may expect. For example, if N=3, Z cannot be larger than 1.155 for any set of values.  More generally, with a  sample of N observations,  Z can never get larger than:

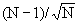
Grubbs and others have tabulated critical values for Z which have been tabulated. The critical value increases with sample size, as expected. If your calculated value of Z is greater than the critical value in the table, then the P value is less than 0.05.

Note that the Grubbs' test only tests the most extreme value in the sample. If it isn't obvious which value is most extreme, calculate Z for all values, but only calculate a P value for Grubbs' test from the largest value of Z.

Prism can compute Grubbs' test with as few as three values in a data set.

How to interpret the P value

If the P value is less than 0.05, it means that there is less than a 5% chance that you'd encounter an outlier so far from the others (in either direction) by chance alone, if all the data were really sampled from a single Gaussian distribution.

Note that the 5% probability (or whatever value of alpha you choose) applies to the entire data set. If your dataset has 100 values, and all are sampled from a Gaussian distribution, there is a 5% chance that the largest (or smallest) value will be declared to be an outlier by Grubbs' test. If you performed outliers tests on lots of data sets, you'd expect this kind of mistake in 5% of data sets.

Don't get confused and think that the 5% applies to each data point. If there are 100 values in the data set all drawn from a Gaussian distribution, there is a 5% chance that Grubbs test will identify the value furthest from the mean as an outlier. This is different than concluding (mistakenly) that you expect 5 of the values (5% of the total) to be mistakenly declared to be outliers.  

References

•B Iglewicz and DC Hoaglin. How to Detect and Handle Outliers (Asqc Basic References in Quality Control, Vol 16) Amer Society for Quality Control, 1993.

•V Barnett, T Lewis, V Rothamsted. Outliers in Statistical Data (Wiley Series in Probability and Mathematical Statistics. Applied Probability and Statistics) John Wiley & Sons, 1994.