Choosing multiple comparisons for two-way ANOVA is not straightforward. Make this choice carefully, and after learning about two-way ANOVA. Consider getting help.
Which kind of comparison?
This is the most important decision. You need to pick a multiple comparison scheme that matches your scientific goal. The pictures, shown below and on the dialog, are probably more helpful than the explanations
The choices of comparisons (in the drop down) depend on the number of rows and columns in your data set.
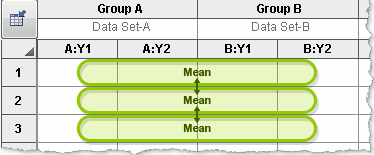
 Compare each cell mean with the other cell mean in that row
Compare each cell mean with the other cell mean in that row
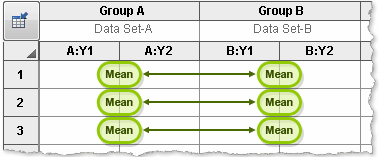
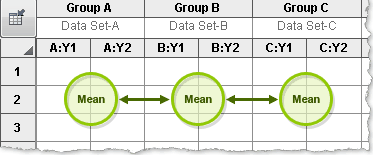
 Compare each cell mean with the other mean in that column
Compare each cell mean with the other mean in that column
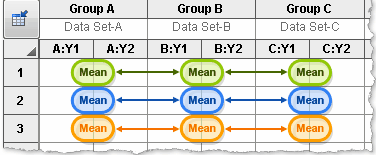
 Simple effects. Within each row, compare columns
Simple effects. Within each row, compare columns
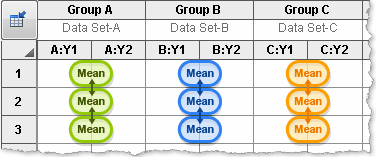
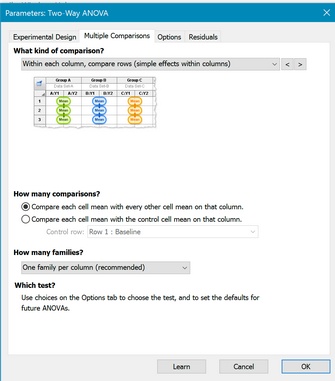
 Simple effects. Within each column, compare rows
Simple effects. Within each column, compare rows
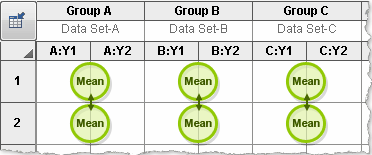
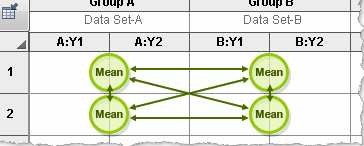
 Compare cell means regardless of rows and columns
Compare cell means regardless of rows and columns
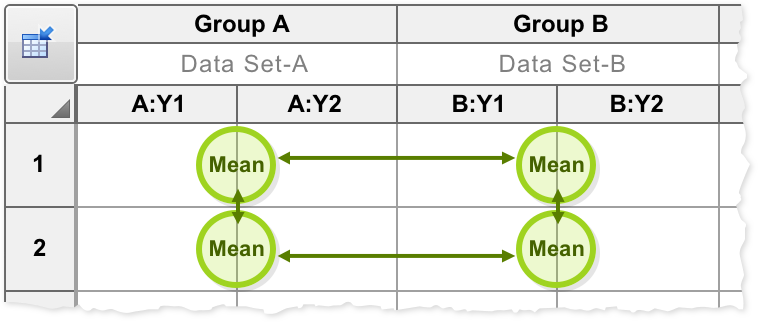
 Compare cell means with others in its row and its column
Compare cell means with others in its row and its column
How many comparisons?
Do you want to compare each mean (in the set) with each other mean? Or only compare each mean to a control mean? The latter approach makes fewer comparisons, so has more power. The choice should be based on experimental design and the scientific questions you are asking.
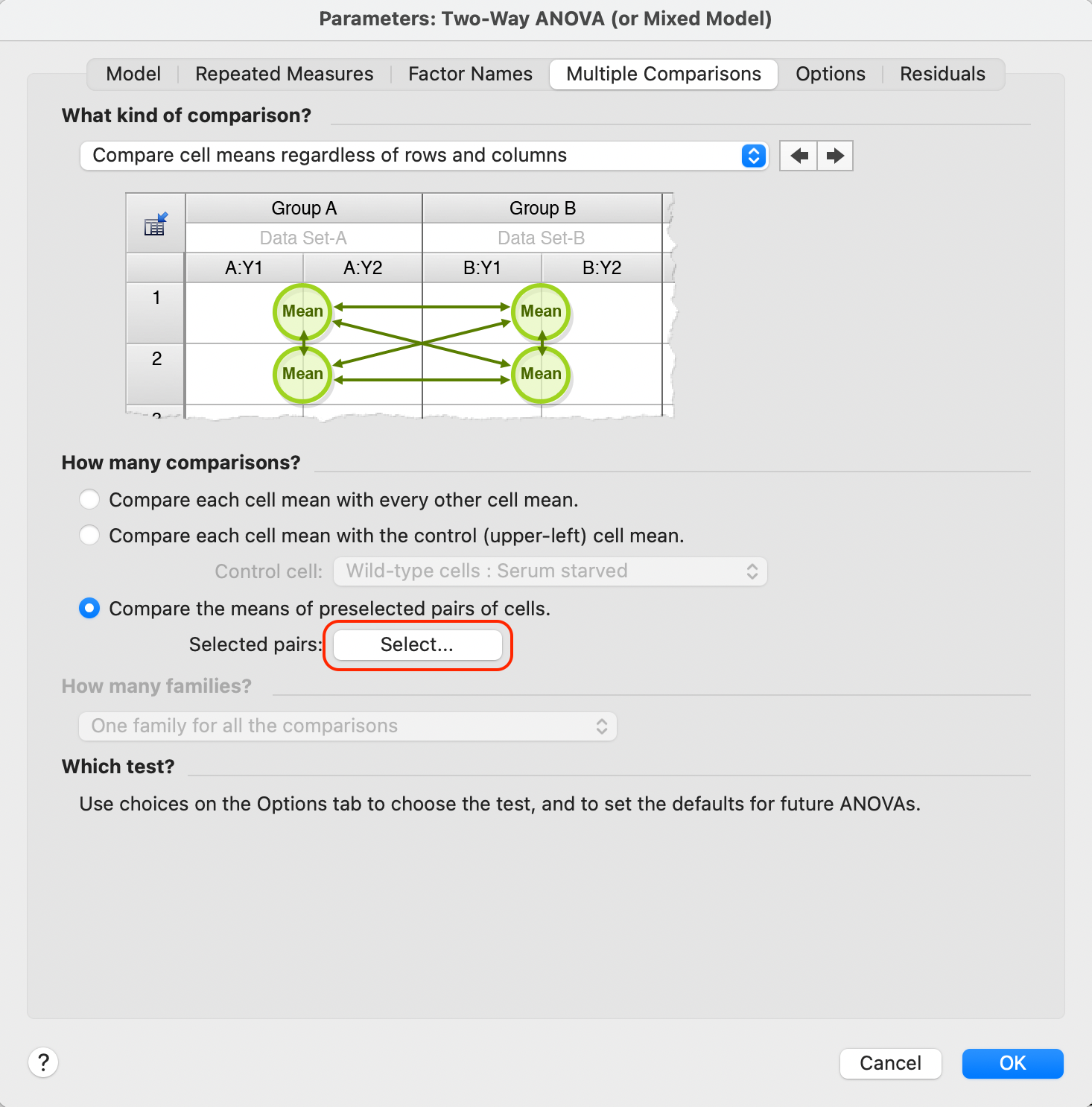
A third option is available for some multiple comparisons methods that allows you to compare the means of preselected pairs of cells. This option is available for:
•Compare row means (main row effect)
•Compare column means (main column effect)
•Compare cell means regardless of rows and columns
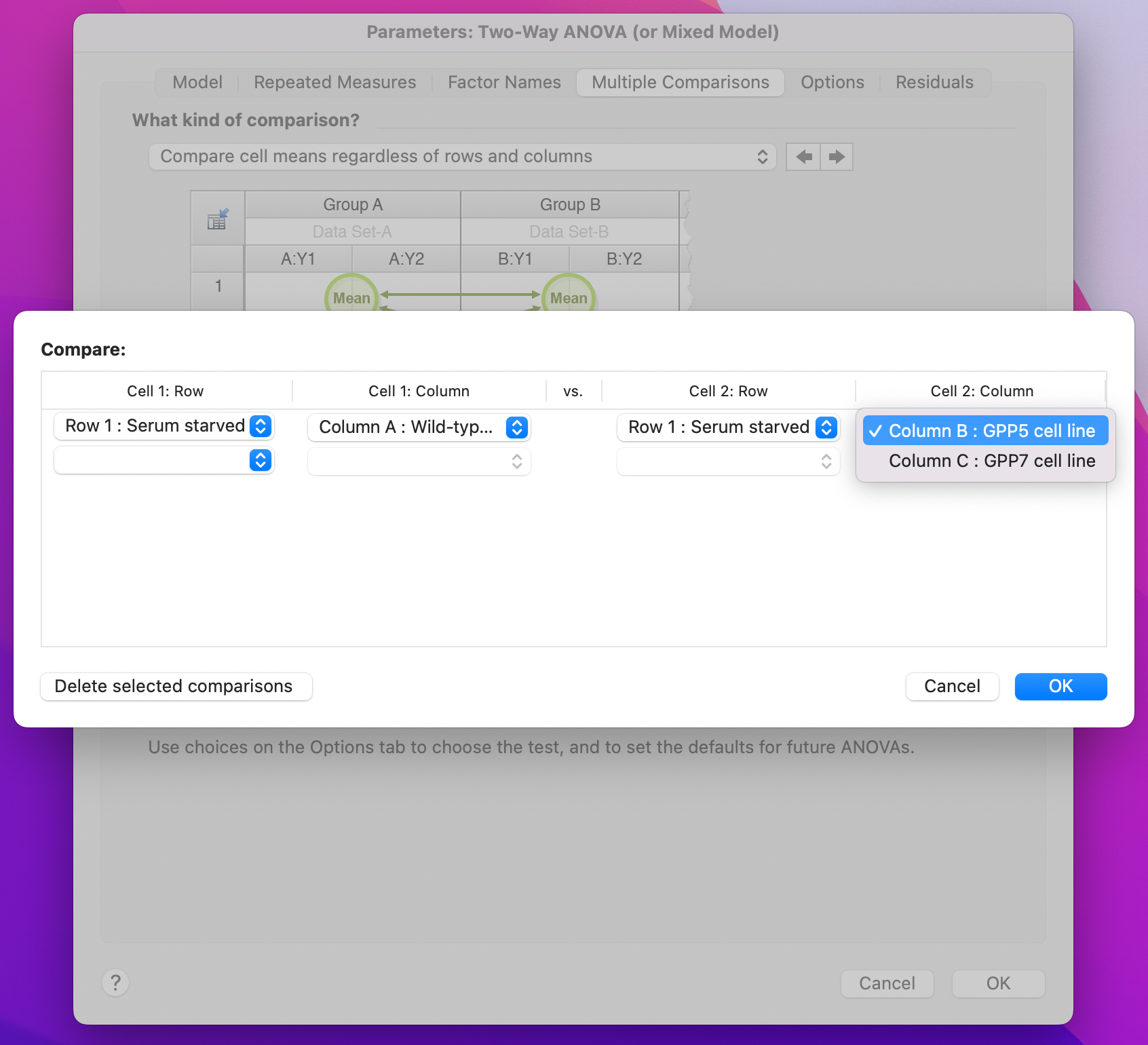
When you choose this option, you'll also need to define the specific comparisons you wish to make. Start by clicking the "Select..." button
In the dialog that appears, you will then specify the rows/columns that define your comparison of interest. Note that Prism will automatically filter from these dropdown menus options that you've either already selected or that don't make sense (for example, you can't compare a cell with itself!).
How many families?
This option is only available for certain multiple comparison choices defined above. These choices include:
•Within each row, compare columns (simple effects within rows)
•Within each column, compare rows (simple effects within columns)
•Compare cell means with others in its row and its column
Why does this option matter? Multiple comparisons take into account the number of comparisons in the family of comparisons. The significance level (alpha) applies to the entire family of comparisons. Similarly, the confidence level (usually 95%) applies to the entire family of intervals, and the multiplicity adjusted P values adjust each P value based on the number of comparisons in a family.
If you choose one of the multiple comparison options listed above, the definition of family is not obvious. Depending on which option you chose, Prism offers different options:
Within each row, compare columns (simple effects within rows)
•One family per row (recommended). With this choice, the comparisons within each row become their own family of comparisons. Consequently, there are the same number of families as there are rows of data. With this choice, there are fewer comparisons per family (but more families), so comparisons have more power. We recommend this choice unless you have strong reason to consider grouping all comparisons into a single family.
•One family for all the comparisons (conservative). With this choice, there is always one family of comparisons regardless of the number of rows in the data. This approach has less power, because it applies a stricter correction for multiple comparisons. This makes sense because there are more comparisons in the family.
Within each column, compare rows (simple effects within columns)
•One family per column (recommended). With this choice, the comparisons within each column become their own family of comparisons. Consequently, there are the same number of families as there are columns of data. With this choice, there are fewer comparisons per family (but more families), so comparisons have more power. We recommend this choice unless you have strong reason to consider grouping all comparisons into a single family.
•One family for all the comparisons (conservative). With this choice, there is always one family of comparisons regardless of the number of columns in the data. This approach has less power, because it applies a stricter correction for multiple comparisons. This makes sense because there are more comparisons in the single family.
Compare cell means with others in its row and its column
•P families. One per row (N) + one per column (M) (recommended). In Prism, the values for "P", "N", and "M" will be given and N + M = P. With this choice, the comparisons within each row become their own family, and the comparisons within each column become their own family. The result is that there are fewer comparisons within each family (but more families), so the comparisons have more power. We recommend this choice unless you have strong reason to consider grouping comparisons into fewer families. Note that selecting this choice generates the same adjusted P values as if you were to choose the multiple comparisons option "Within each row, compare columns (simple effects within rows)" with one family per row and separately choose the multiple comparisons option "Within each column, compare rows (simple effects within columns" with one family per column.
•2 families. All comparisons within rows (1) + all within columns (1) (more conservative). With this choice, all comparisons within rows will be grouped into a single family, while all comparisons within columns will be grouped into a different family. This choice has more power than the "1 family" choice (below), but less power than the recommended choice to have families within each row and within each column (above). Note that selecting this choice generates the same adjusted P values as if you were to choose the multiple comparisons option "Within each row, compare columns (simple effects within rows)" with the "One family for all the comparisons" option and separately choose the multiple comparisons option "Within each column, compare rows (simple effects within columns)" with the "One family for all the comparisons" option.
•1 family. All comparisons (most conservative). With this choice, there is always one family of comparisons regardless of the number of rows or columns in the data. This approach has less power than either of the others because it applies a stricter correction for multiple comparisons. This makes sense because there are more comparisons in the single family.
Additional information
The results page will repeat your choice for the number of families to use, so it is clear how to interpret the results.
Prism 5.04 and 5.0d use the "One family per row/column" definition of family (and do not offer you a choice of other definitions). If you wish to compare results with Prism 5, note this bug in releases of Prism 5 prior to 5.04 (Windows) and 5.0d (Mac).