Example data

Motulsky et al. asked whether people with hypertension (high blood pressure) had altered numbers of alpha2-adrenergic receptors on their platelets (Clinical Science 64:265-272, 1983). There are many reasons to think that autonomic receptor numbers may be altered in hypertension. We studied platelets because they are easily accessible from a blood sample. The results are shown here:

 

The two means were almost identical, so of course a t test computed a very high P value. We concluded that there is no statistically significant difference between the number of alpha2 receptors on platelets of people with hypertension compared to controls. When we published this over 40 years ago, we did not go further.

These negative data can be interpreted in terms of confidence intervals or using power analyses. The two are equivalent and are just alternative ways of thinking about the data.

Interpreting not significant results using a confidence interval

All results should be accompanied by confidence intervals showing how well you have determined the differences (ratios, etc.) of interest. For our example, the 95% confidence interval for the difference between group means extends from -45 to 57 receptors/platelet. Once we accept the assumptions of the t test analysis, we can be 95% sure that this interval contains the true difference between mean receptor number in the two groups. To put this in perspective, you need to know that the average number of receptors per platelet is about 260.

The interpretation of the confidence interval must be in a scientific context. Here are two very different approaches to interpreting this confidence interval.

•The CI includes possibilities of a 20% change each way. A 20% change is huge. With such a wide CI, the data are inconclusive. Could be no change. Could be big decrease. Could be big increase.

•The CI tells us that the true difference is unlikely to be more than 20% in each direction. Since we are only interested in changes of 50%, we can conclude that any difference is, at best, only 20% or so, which is biologically trivial. These are solid negative results.

Both statements are sensible. It all depends on how you would interpret a 20% change. Statistical calculations can only compute probabilities. It is up to you to put these in a scientific context. As with power calculations, different scientists may interpret the same results differently.

Interpreting not significant results using power analysis

What was the power of this study to find a difference (if there was one)? The answer depends on how large the difference really is. Here are the results shown as a graph.

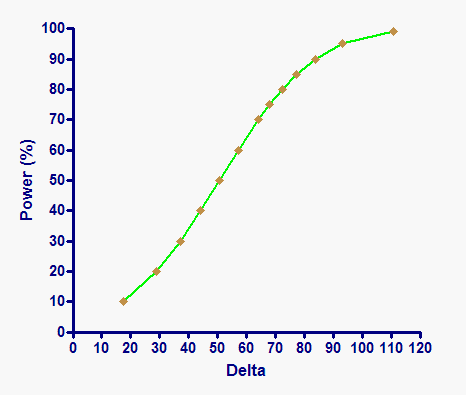
All studies have a high power to detect "big" differences and a low power to detect "small" differences, so power graph all have the same shape. Interpreting the graph depends on putting the results into a scientific context. Here are two alternative interpretations of the results:

•We really care about receptors in the heart, kidney, brain and blood vessels, not the ones in the platelets (which are much more accessible). So we will only pursue these results (do more studies) if the difference was 50%. The mean number of receptors per platelet is about 260, so we would only be seriously interested in these results if the difference exceeded half of that, or 130. From the graph above, you can see that this study had extremely high power to detect a difference of 130 receptors/platelet. In other words, if the difference really was that big, this study (given its sample size and variability) would almost certainly have found a statistically significant difference. Therefore, this study gives convincing negative results.

•Hey, this is hypertension. Nothing is simple. No effects are large. We've got to follow every lead we can. It would be nice to find differences of 50% (see above) but realistically, given the heterogeneity of hypertension, we can't expect to find such a large difference. Even if the difference was only 20%, we'd still want to do follow up experiments. Since the mean number of receptors per platelet is 260, this means we would want to find a difference of about 50 receptors per platelet. Reading off the graph (or the table), you can see that the power of this experiment to find a difference of 50 receptors per cell was only about 50%. This means that even if there really were a difference this large, this particular experiment (given its sample size and scatter) had only a 50% chance of finding a statistically significant result. With such low power, we really can't conclude very much from this experiment. A reviewer or editor making such an argument could convincingly argue that there is no point publishing negative data with such low power to detect a biologically interesting result.

As you can see, the interpretation of power depends on how large a difference you think would be scientifically or practically important to detect. Different people may reasonably reach different conclusions. Note that it doesn't help at all to look up the power of a study to detect the difference we actually observed. This is a common misunderstanding.

Comparing the two approaches

Confidence intervals and power analyses are based on the same assumptions, so the results are just different ways of looking at the same thing. You don't get additional information by performing a power analysis on a completed study, but a power analysis can help you put the results in perspective

The power analysis approach is based on having an alternative hypothesis in mind. You can then ask what was the probability that an experiment with the sample size actually used would have resulted in a statistically significant result if your alternative hypothesis were true.

If your goal is simply to understand your results, the confidence interval approach is enough. If your goal is to criticize a study of others, or plan a future similar study, it might help to also do a power analysis.

Reference

1. Motulsky HJ, O'Connor DT, Insel PA. Platelet alpha 2-adrenergic receptors in treated and untreated essential hypertension.  Clin Sci (Lond). 1983 Mar;64(3):265-72.