Before you can test for equivalence, you first have to define a range of treatment effects that you consider to be scientifically or clinically trivial. You must set this range based on scientific or clinical judgment -- statistical analyses can't help.

If the treatment effect you observed is outside this zone of scientific or clinical indifference, then clearly you can't conclude the treatments are equivalent.

If the treatment effect does lie within the zone of clinical or scientific indifference, then you can ask whether the data are tight enough to make a strong conclusion that the treatments are equivalent.

Testing for equivalence with confidence intervals.

The figure below shows the logic of how to test for equivalence with confidence intervals. The horizontal axis shows the absolute value of the treatment effect (difference between mean responses). The filled circles show the observed effect, which is within the zone of indifference. The horizontal error bars show the one-sided 95% confidence intervals, which show the largest treatment effect consistent with the data (with 95% confidence).

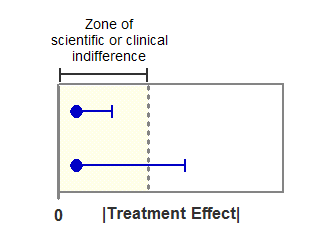
In the experiment shown on top, even the limit of the confidence interval lies within the zone of indifference. You can conclude (with 95% confidence) that the two treatments are equivalent.

In the experiment shown on the bottom, the confidence interval extends beyond the zone of indifference. Therefore, you cannot conclude that the treatments are equivalent. You also cannot conclude that the treatments are not equivalent, as the observed treatment is inside the zone of indifference. With data like these, you simply cannot make any conclusion about equivalence.

Testing for equivalence using statistical hypothesis testing

Thinking about statistical equivalence with confidence intervals (above) is pretty straightforward. Applying the ideas of statistical hypothesis testing to equivalence is much trickier.

Statistical hypothesis testing starts with a null hypothesis, and then asks if you have enough evidence to reject that null hypothesis. When you are looking for a difference, the null hypothesis is that there is no difference. With equivalence testing, we are looking for evidence that two treatments are equivalent. So the “null” hypothesis, in this case, is that the treatments are not equivalent, but rather that the difference is just barely large enough to be outside the zone of scientific or clinical indifference.

In the figure above, define the null hypothesis to be that the true effect equals the effect denoted by the dotted line. Then ask: If that null hypothesis were true, what is the chance (given sample size and variability) of observing an effect as small or smaller than observed. If the P value is small, you reject the null hypothesis of nonequivalence, so conclude that the treatments are equivalent. If the P value is large, then the data are consistent with the null hypothesis of nonequivalent effects.

Since you only care about the chance of obtaining an effect so much lower than the null hypothesis (and wouldn't do the test if the difference were higher), you use a one-tail P value.

The graph above is plotted with the absolute value of the effect on the horizontal axis. If you plotted the treatment effect itself, you would have two dotted lines, symmetric around the 0 point, one showing a positive treatment effect and the other showing a negative treatment effect. You would then have two different null hypotheses, each tested with a one-tail test. You'll see this referred to as Two One-Sided Tests Procedure (1, 2).

The two approaches are equivalent

Of course, using the 95% confidence interval approach (using one-sided 95% confidence intervals) and the hypothesis testing approach (using one-sided 0.05 threshold for significance are completely equivalent, so always give the same conclusion. The confidence interval seems to me to be far more straightforward to understand.

Testing for equivalence with Prism

Prism does not have any built-in tests for equivalence. But you can use Prism to do the calculations:

1.Compare the two groups with a t test (paired or unpaired, depending on experimental design).

2.Check the option to create 90% confidence intervals. That's right 90%, not 95%.

3.If the entire range of the 90% confidence interval lies within the zone of indifference that you defined, then you can conclude with 95% confidence that the two treatments are equivalent.

References

1. D.J. Schuirmann, A comparison of the Two One-Sided Tests Procedure and the Power Approach for assessing the equivalence of average bioavailability, J. Pharmacokinetics and pharmacodynamics, 115: 1567, 1987.

2. S. Wellek,  Testing Statistical Hypotheses of Equivalence, Chapman and Hall/CRCm, 2010, ISBN: 978-1439808184.