Key facts about the geometric mean

•Prism computes the geometric mean by computing the logarithm of all values, then calculating the mean of the logarithms, and finally taking the antilog.

•Prism uses base 10 (common) logarithms, and then takes ten to the power of the mean of the logarithms to get the geometric mean. Some programs use natural logs and then use the exponential function to convert back.

•Using logarithms and antilogarithms is equivalent to multiplying all the values together and taking that product to the 1/n power, where n is the number of values. You'll see this definition in some books.

•The geometric mean cannot be computed if any values are zero or negative.

•The geometric mean is in the same units as the data and the arithmetic mean.

•The geometric mean is never larger than the arithmetic mean.

•If the data are sampled from a lognormal distribution, the geometric mean is probably the best way to express the center of the distribution.

Geometric SD factor

Prism (introduced in Prism 7) reports a Geometric SD factor when you request a geometric mean. It also can plot the geometric mean and its geometric SD factor on some graphs.

Key facts about the geometric SD factor:

•The term geometric SD is not commonly used. It was introduced by Kirkwood (1).

•How the geometric SD is computed: First, transform all the values to logarithms, compute the sample SD of those log values, and then take the antilogarithm of that SD.  

•The geometric SD factor has no units. It is a unitless ratio.

•You can't add the geometric SD to the geometric mean (or any other value), and makes equally no sense to ever subtract the geometric SD from the geometric mean. The geometric SD is a value you always multiply or divide by. This is very different than a ordinary SD which has the same units as the data, so can be added to or subtracted from the mean.

•The range from (the geometric mean divided by the geometric SD factor) to (the geometric mean multiplied by the geometric SD factor) will contain about two thirds of the values if the data are sampled from a lognormal distribution. Similarly, the range from (the mean minus the SD) to (the mean plus the SD) will contain about two thirds of the values when data are sampled from a Gaussian distribution.  

•It is rare to see publications show the geometric SD. It is common to see a result reported as "The mean is 3.2 ± 1.2 (SD)". However it is currently rare to report that the geometric mean is 4.3 *÷ 1.14. Instead of a "plus or minus" symbol, I entered a "times or divided by" symbols.

•While it seems odd to express an error as "multiplied or divided by", it is really no stranger than "plus or minus".

Example

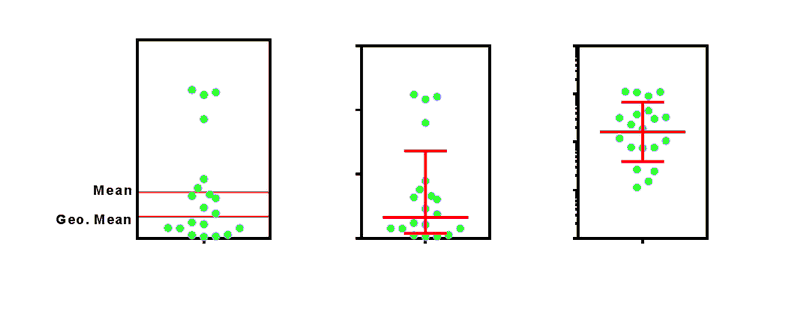
The graph above plots 20 values sampled from a lognormal distribution. The graph on the left shows you that the mean and geometrical mean are very different. The middle graph plots the geometric mean with error bars computed as the geometric mean times or divided by the geometric SD factor. The graph shows the same thing with a logarithmic Y axis. Now the distribution looks symmetrical, and the error bars seem to extend the same distance in each direction. But the ends of the error bars are at the same Y value in the middle and right graph. The right graph uses a logarithmic axis.

Reference

1. Kirkwood, TBL (1979). "Geometric means and measures of dispersion". Biometrics 35: 908–9.