Key facts about the hazard ratio
•The hazard is the frequency at which the event of interest occurs per unit of time, and can be generally thought of as the “slope” of the survival curve. It is a measure of how rapidly subjects are experiencing the event of interest
•The hazard ratio is a comparison of the hazard between two groups. If the hazard ratio is 2.0, then the rate of the event occurring in one group is twice the rate of the other group
•The hazard ratio is not computed at any single time point, but is computed from all of the data contained within the survival curve
•Since there is only one hazard ratio reported, it can only be interpreted if you assume that the population hazard rate is consistent over time, and that any differences are due to random sampling. This is called the assumption of proportional hazards and is a fundamental assumption in Cox proportional hazards regression
•If the hazard rate is not consistent over time, the value that Prism reports for the hazard ratio will not be useful. If two survival curves cross, the hazard rates are certainly not consistent (an exception to this is if the curves cross at late time points, when there are few subjects still being followed and as a result there is a lot of uncertainty in the true position of the survival curves)
•The hazard ratio is not directly related to the ratio of median survival times. A hazard ratio of 2.0 does not mean that the median survival time is doubled (or halved). A hazard ratio of 2.0 means that a subject in one group who has not experienced the event of interest at a given time point has double the probability of having experienced the event by the next point compared to a subject in the other group.
•Prism computes the hazard ratio - and its confidence interval - using two methods which are explained below. For each method, Prism reports both the hazard ratio and its reciprocal. If subjects in Group A experience the event of interest at twice the rate of subjects in Group B (i.e. HR=2.0), then subjects in Group B will - by definition - experience the event of interest at half the rate of subjects in Group A (HR=1/2.0=0.5)
•For other cautions about interpreting hazard ratios, see two reviews by Hernan (1) and Spruance (2)
•Duerden (6) wrote a good, easy-to-follow explanation of hazard ratios
The two methods compared
Prism reports the hazard ratio computed by two different methods: logrank and Mantel-Haenszel. These two methods usually give identical (or nearly identical) results. However, the results can differ when several subjects experience the event of interest at the same time (so-called “tied observations”) or when the hazard ratio is far from 1.0.
Bernstein and colleagues analyzed simulated data with both methods (3). In all of their simulations, the assumption of proportional hazards was true, and the two methods generated very similar values. The logrank method (which they refer to as the O/E method) reports values that are closer to 1.0 than the true hazard ratio, especially when the hazard ratio is large or the sample size is large.
When there are ties, both methods are less accurate. The logrank method tends to report hazard ratios that are even closer to 1.0 (so the reported hazard ratio is too small when it is reported as greater than 1.0, and too large when reported as less than 1.0). In contrast, the Mantel-Haenszel method reports hazard ratios that are further from 1.0 (so the reported hazard ratio is too large when it is reported as greater than 1.0, and too small when reported as less than 1.0).
What does it mean when the two hazard ratios are very different?
The simulations of Bernstein and colleagues (3) did not compare the two methods with data simulated where the assumption of proportional hazards was not true. In a separate example of data where the proportional hazards assumption was dubious at best, the hazard ratios between the two methods were very different (by a factor of three). It seems that the Mantel-Haenszel method gives more weight to differences in the hazard rate at later time points, while the logrank method gives equal weight to all time points.
If you observe very different hazard ratio values with these two methods, think about whether the assumption of proportional hazards is reasonable. If that assumption is not reasonable, then the entire concept of a single hazard ratio describing the entire curve is not meaningful.
How the hazard ratio is computed
The logrank and Mantel-Haenszel methods that Prism utilized to report hazard ratios are very similar. Both are explained in chapter 3 of Machin, Cheung, and Parmar; Survival analysis (4).
The Mantel Haenszel approach:
1.Compute the total variance, V, as explained on page 38-40 of a handout by Michael Vaeth
2.Compute
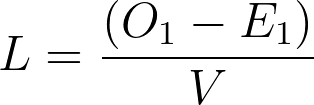
Where O1 is the total observed number of events in Group 1, and E1 is the expected number of events in Group 1. You’d get the same value of L if using the other group
3.Note that L is the natural logarithm of the hazard ratio. So
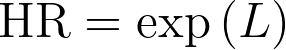
4.The lower 95% confidence limit of the hazard ratio equals
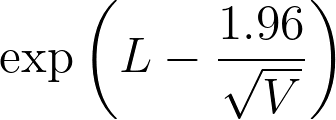
5.The upper 95% confidence limit of the hazard ratio equals
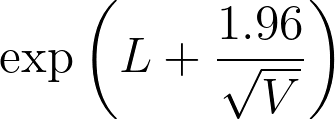
The logrank approach:
1.As part of the Kaplan-Meier calculations, compute the number of observed events (often deaths) in each group (Oa for observed number of events in Group A and Ob for observed number of events in Group B), and the expected number of events assuming a null hypothesis of no difference in survival (Ea for expected number of events in Group A and Eb for expected number of events in Group B)
2.The hazard ratio is then
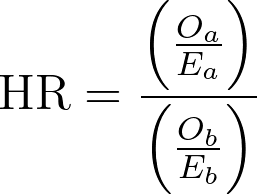
3.Calculate the natural logarithm of the hazard ratio
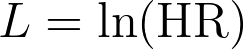
4.The standard error of the natural logarithm of the hazard ratio is
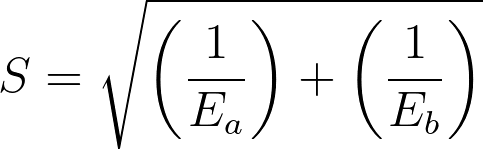
5.The lower 95% confidence limit of the hazard ratio equals
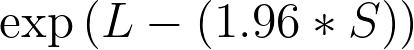
6.The upper 95% confidence limit of the hazard ratio equals
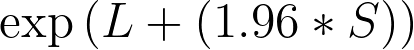
Prior versions of Prism
Prism 6 reported hazard ratios computed using both the Mantel-Haenszel and the logrank methods. In each of these methods, the natural logarithm of the hazard ratio (denoted L in the calculations above) is used to calculate the upper and lower 95% confidence limits. A bug in Prism 6 resulted in the Mantel-Haenszel approach when calculating the confidence limits for hazard ratio from the logrank method. Usually the differences in HRs were small, so this bug was mostly trivial. It only affected the calculations when the two HR values were very different. In these situations, one has to wonder if either definition is very helpful, as it's likely that - in these cases - the data simply don’t comply with the assumption of proportional hazards. This bug was fixed in version 7.00 (Windows) and 7.0a (Mac).
Prism 5 computed the hazard ratio and its confidence interval using the Mantel-Haenszel approach. Prism 4 used the logrank method to compute the hazard ratio, but used the Mantel-Haenszel approach to calculate the confidence interval of the hazard ratio. The results can be inconsistent. In rare cases, the hazard ratio reported by Prism 4 could be outside the confidence interval of the reported hazard ratio.
References
1.M.A. Hernán. Hazards of Hazard Ratios, Epidemiology. 21:13-5, 2010.
2.S. L. Spruance et all, Hazard ratio in clinical trials, Antimicrobial Agents and Chemotherapy vol. 48 (8) pp. 2787, 2004.
3.L Bernstein, J. Anderson and MC Pike. Estimation of the proportional hazard in two-treatment-group clinical trials. Biometrics (1981) vol. 37 (3) pp. 513-519
4.David Machin, Yin Bun Cheung, Mahesh Parmar, Survival Analysis: A Practical Approach, 2nd edition, IBSN:0470870400.
5.Michael Vaeth, Statistical analysis of survival data in clinical research (2004).
6.Martin Duerden, What are hazard ratios? (2009 )