The appeal of choosing sample size as you go
To many, calculating sample size before the study starts seems like a nuisance. Why not do the analyses as you collect data? If your results are not statistically significant, then collect some more data, and reanalyze. If your results are statistically significant result, then stop the study and don't waste time or money on more data collection.
The problem with this approach is that you'll keep going if you don't like the result, but stop if you do like the result. The consequence is that the chance of obtaining a "significant" result if the null hypothesis were true is a lot higher than 5%.
Simulation to show the dangers of not choosing sample size in advance
The graph below illustrates this point via simulation. We simulated data by drawing values from a Gaussian distribution (mean=40, SD=15, but these values are arbitrary). Both groups were simulated using exactly the same distribution. We picked N=5 in each group and computed an unpaired t test and recorded the P value. Then we added one subject to each group (so N=6) and recomputed the t test and P value. We repeated this until N=100 in each group. Then we repeated the entire simulation three times. These simulations were done comparing two groups with identical population means. So any "statistically significant" result we obtain must be a coincidence -- a Type I error.
The graph plots P value on the Y axis vs. sample size (per group) on the X axis. The greenish shaded area at the bottom of the graph shows P values less than 0.05, so deemed "statistically significant".
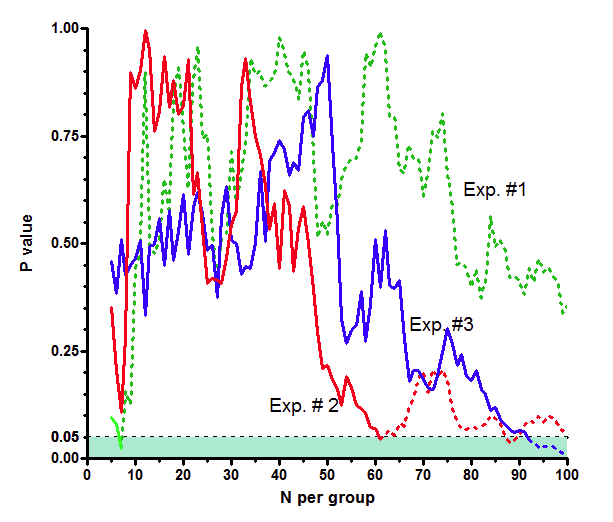
The green curve shows the results of the first simulated set of experiments. It reached a P value less than 0.05 when N=7, but the P value is higher than 0.05 for all other sample sizes. The red curve shows the second simulated experiment. It reached a P value less than 0.05 when N=61 and also when N=88 or 89. The blue curve is the third experiment. It has a P value less than 0.05 when N=92 to N=100.
If we followed the sequential approach, we would have declared the results in all three experiments to be "statistically significant". We would have stopped when N=7 in the green experiment, so would never have seen the dotted parts of its curve. We would have stopped the red experiment when N=61, and the blue experiment when N=92. In all three cases, we would have declared the results to be "statistically significant".
Since these simulations were created for values where the true mean in both populations was identical, any declaration of "statistical significance" is a Type I error. If the null hypothesis is true (the two population means are identical) we expect to see this kind of Type I error in 5% of experiments (if we use the traditional definition of alpha=0.05 so P values less than 0.05 are declared to be significant). But with this sequential approach, all three of our experiments resulted in a Type I error. If you extended the experiment long enough (infinite N) all experiments would eventually reach statistical significance. Of course, in some cases you would eventually give up even without "statistical significance". But this sequential approach will produce "significant" results in far more than 5% of experiments, even if the null hypothesis were true, and so this approach is invalid.
Bottom line
It is important that you choose a sample size and stick with it. You'll fool yourself if you stop when you like the results, but keep going when you don't. If experiments continue when results are not statistically significant, but stop when the results are statistically significant, the chance of mistakenly concluding that results are statistical significant is far greater than 5%.
There are some special statistical techniques for analyzing data sequentially, adding more subjects if the results are ambiguous and stopping if the results are clear. Look up 'sequential medical trials' in advanced statistics books to learn more.