Hierarchical clustering involves creating clusters by merging observations or existing clusters together with other observations or clusters based on their similarities. In order to perform hierarchical clustering, you must define both a method to calculate distances as well as a linkage method. When determining the distance between two individual objects (not clusters), it’s straightforward to specify which points to use to calculate the distance: simply use the location of the two objects. However, when trying to calculate the distance between an individual object and a cluster - or two clusters - it’s no longer as straightforward. There are many different ways to select points to use to calculate the distance between two clusters or between a cluster and an individual object. These different approaches are the linkage methods, and Prism offers a number of different options.

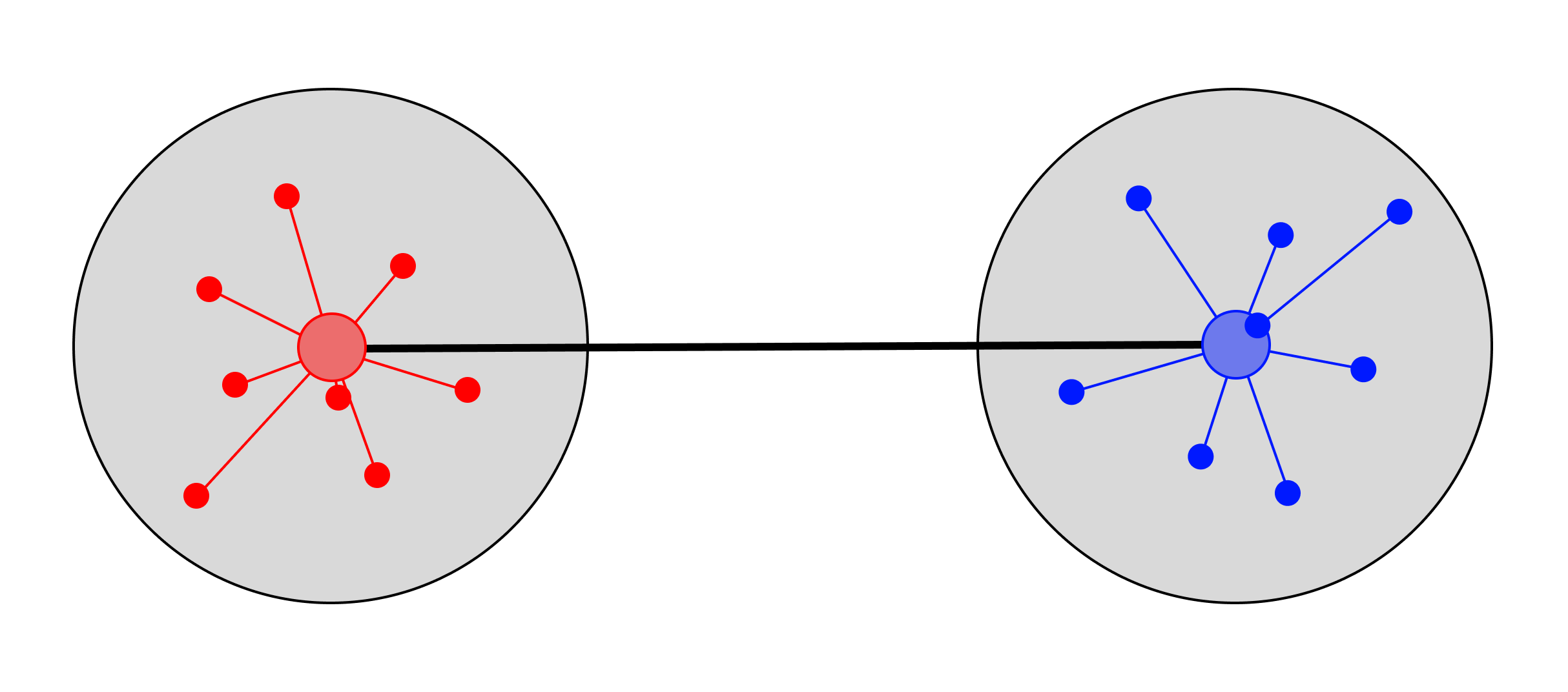
Complete Linkage

When using complete linkage, the distance between clusters is defined as the maximum distance between any pair of points, one from each cluster. This method tends to produce compact, spherical clusters, but may be sensitive to outliers.

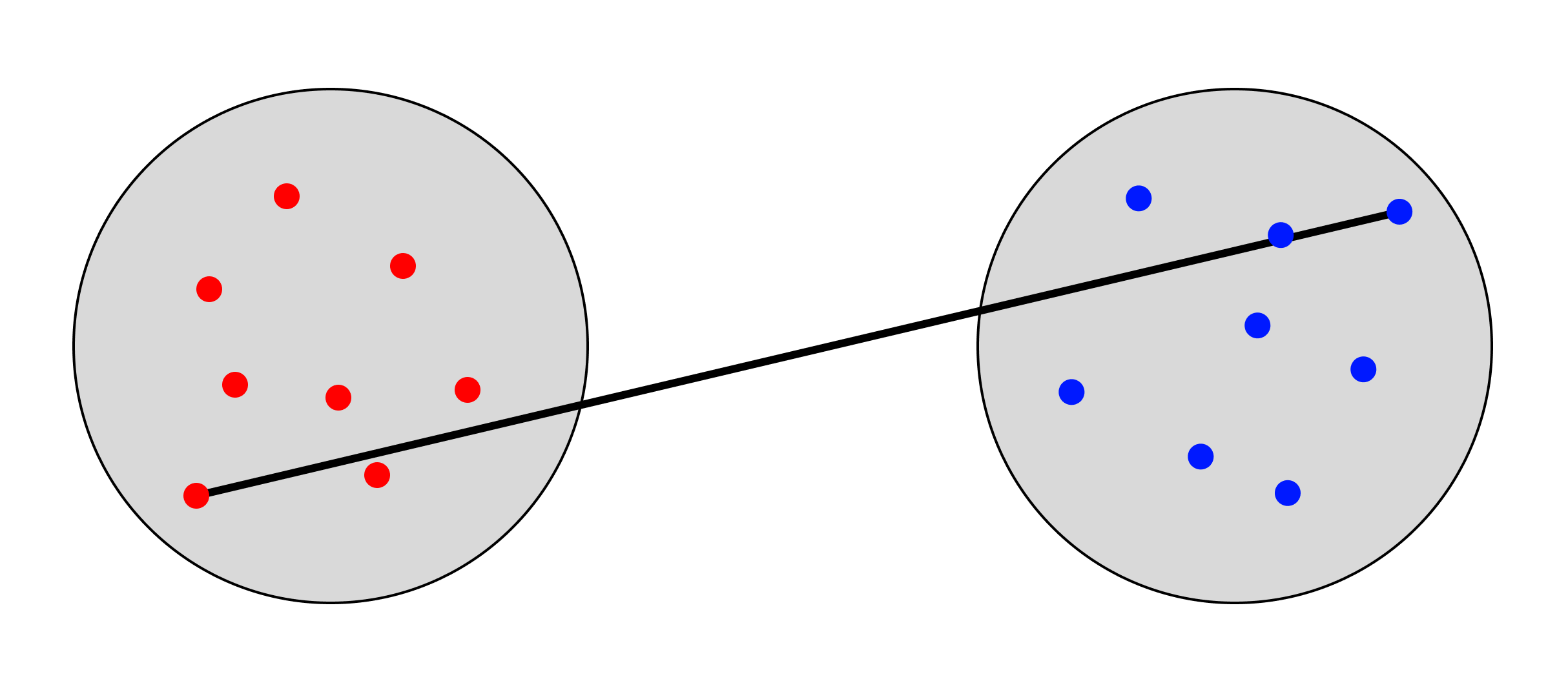
Single Linkage

In contrast to complete linkage, single linkage defines the distance as the minimum distance between any pair of points, one from each cluster. This method is capable of handling more irregularly shaped clusters, but may potentially result in “long” clusters caused by chaining points together during clustering.

Simple Average

The simple average linkage method attempts to strike a balance between the complete and single linkage methods. For this approach, consider Cluster C that was formed by joining Clusters A and B in a previous step. Using the simple average linkage method, the distance from Cluster C to another cluster (Cluster D) is the average of the mean distance between the elements of Cluster A to the elements of Cluster D and the elements of Cluster B to cluster D.

Note that in this approach, the average distance is calculated without taking into consideration the number of elements within each “child” cluster. Because of this, clusters with more elements contribute more unevenly to the final distance calculation, and this method is sometimes referred to as the weighted pair group method with arithmetic mean (or WPGMA) method. Note that “weighted” here refers to the result of the calculation and not to the formula itself since no weights were applied to the distance calculations to account for the sizes of each cluster. In some applications, this method is sometimes also referred to as the “McQuitty” method.

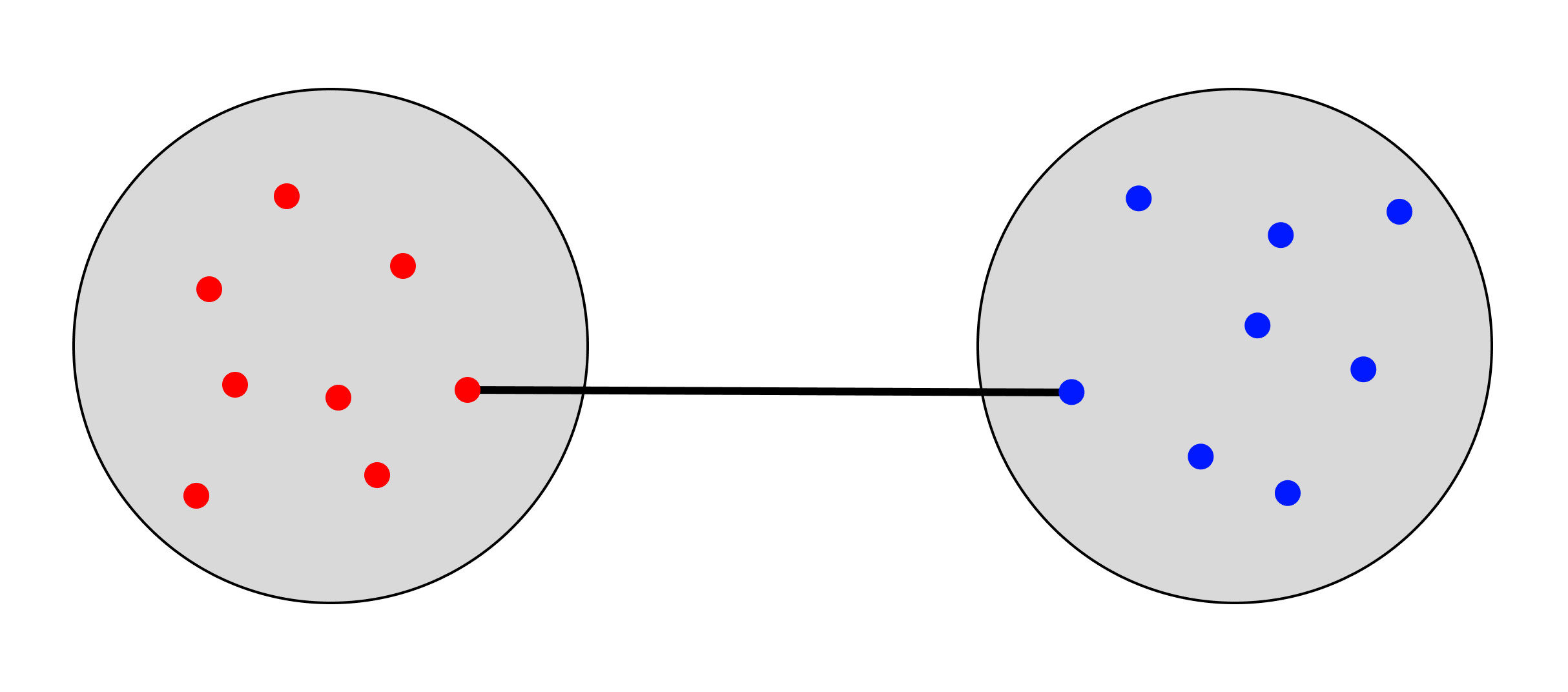
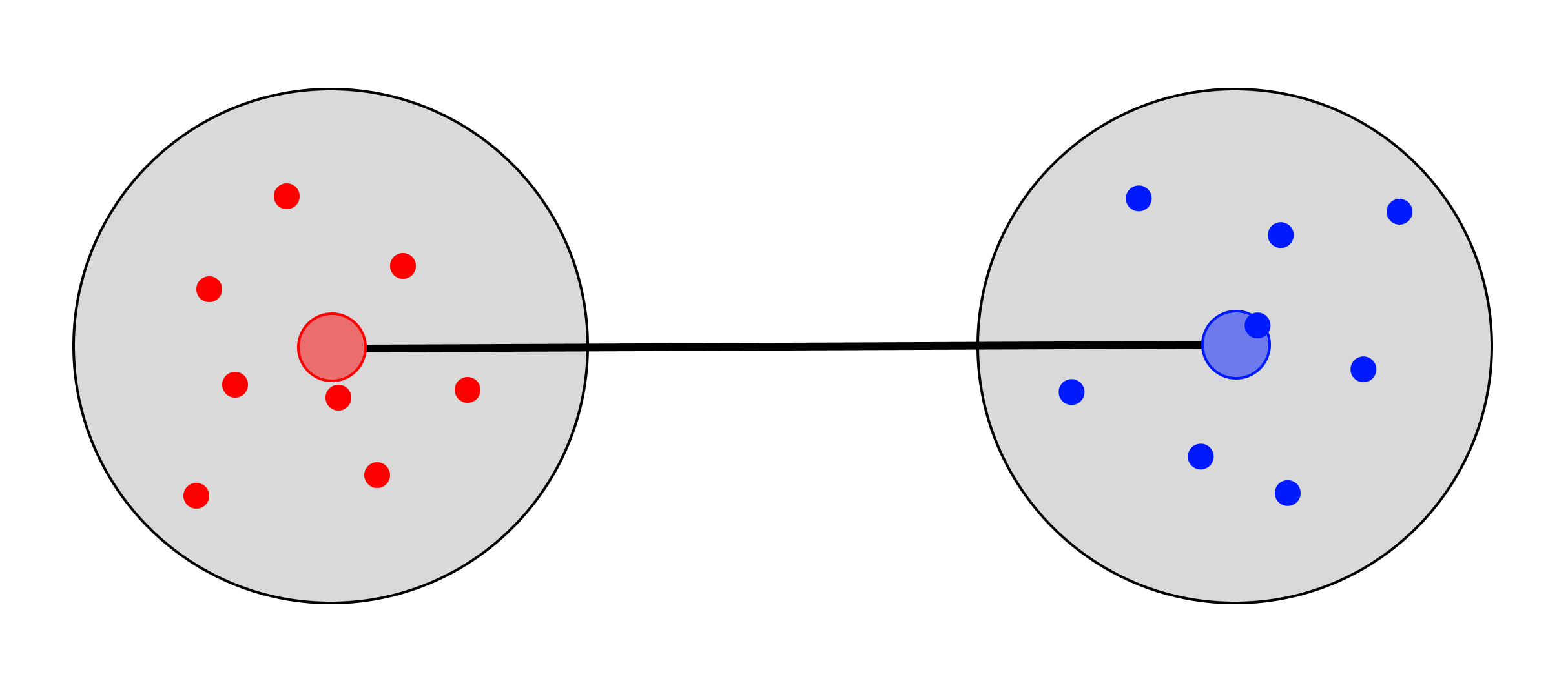
Centroid

The centroid linkage method first calculates the centroid of all clusters, and then defines the distance as the distance between these centroids.

To find the centroid, the average values of each point within the cluster are determined. While this might seem similar to using the average distance between each set of points, this method is distinct from both the simple average and group average approaches, and will generate different clustering results in most situations.

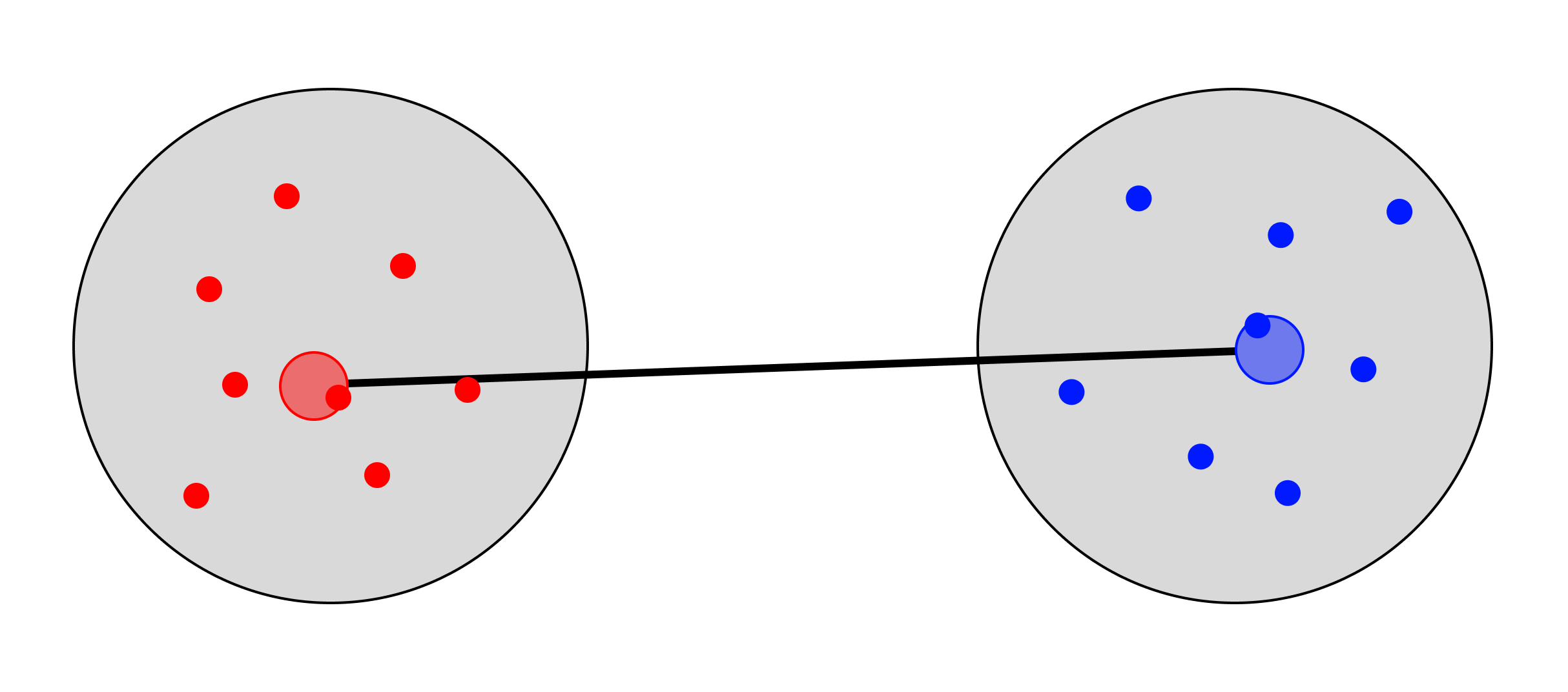
Median

The median linkage method is very similar to the centroid method in that the “center” of each cluster is first defined, then the distance is defined as the distance between each cluster center.

The difference in this case is that instead of using the average of the values in each cluster to define the center point, the median of these values is used instead. Because the median is used rather than the average, the median method can be somewhat less sensitive to outliers when compared to the centroid method.

Group Average

Like the simple average method, the group average linkage method also considers the pairwise distance between all points of each cluster being merged.

The distinction between these two methods is that the group average considers the number of points in each cluster, and weights the distances by these sizes. By applying these weights in the formula, the result is said to be “unweighted” (an unfortunate and confusing bit of terminology). As a result, this method is sometimes called the unweighted pair group method with arithmetic mean or UPGMA.

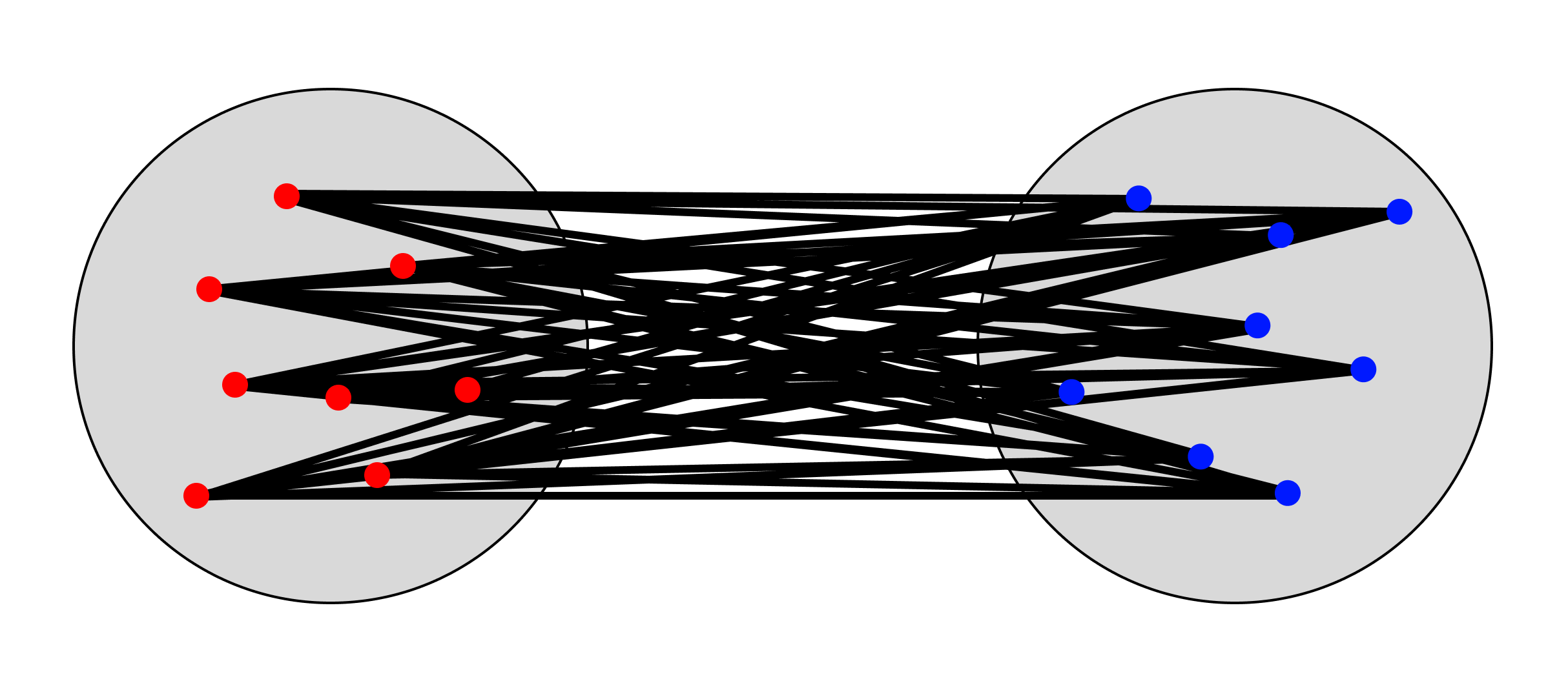
Ward’s method

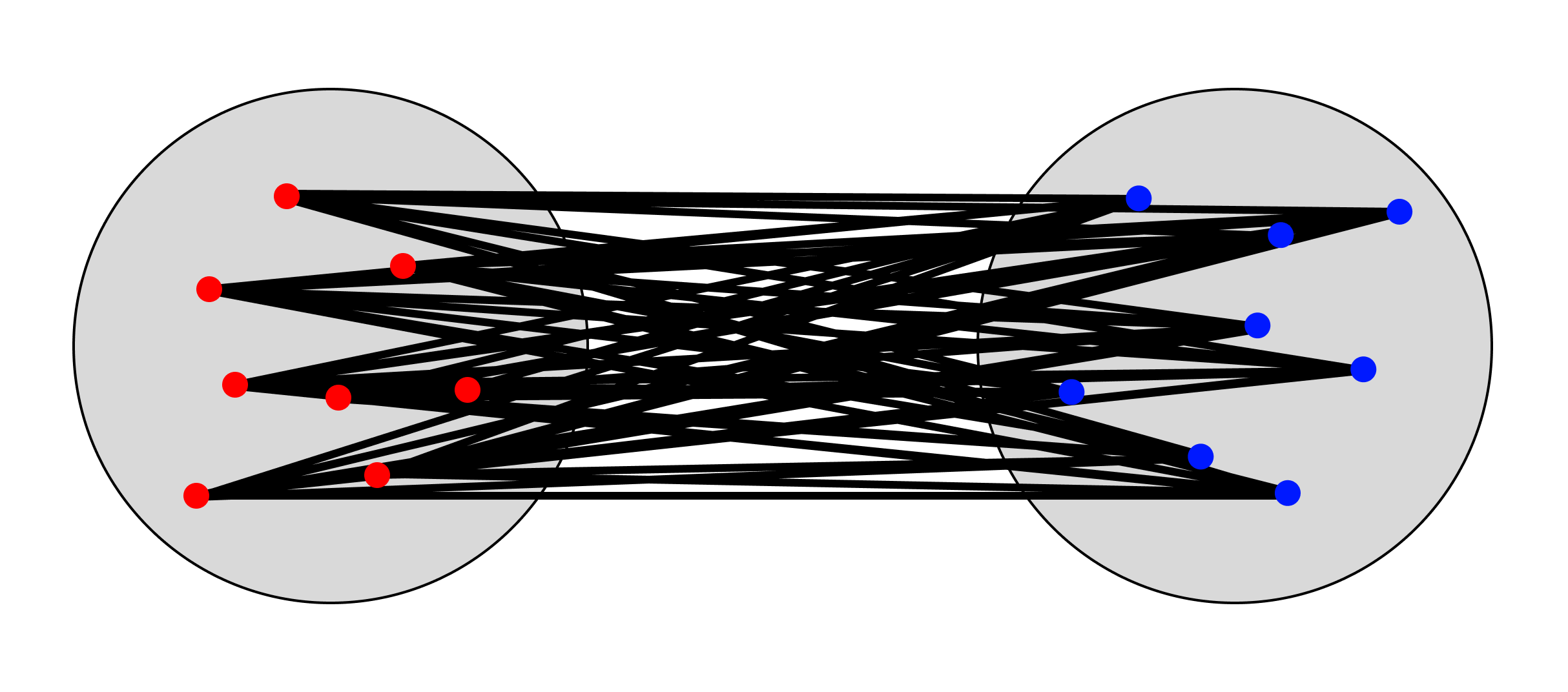
Ward’s method involves the formation of clusters in a way that minimizes the variance within each cluster. At each step during the clustering process, two clusters are merged in a manner that results in the smallest increase in the total sum of squared distances between the points of the resulting cluster. Of the different linkage methods provided, this one is often the most computationally intensive, but can perform well when data contain clusters of varying sizes and densities. Note however that Ward’s method can be sensitive to outliers as these will have large impacts on the total sum of squared distances.

In essence, Ward's method attempts to minimize the red/blue lines within clusters in the image below, and as a result maximizes the black lines between clusters.