1. Create a Column table

From the Welcome or New Table dialog, choose the Column tab.

2. Enter the P values

Enter P values, calculated elsewhere, into column A.

Every value must be a P value (between 0.0 and 1.0). You cannot enter "<0.0001" or "ns" or "**". Each P value you enter must be a decimal fraction.

Optionally, enter a column title adjacent to each P value to identify the corresponding comparison. This will make it easier to understand the results. If you don't enter row titles, Prism will label the results using the original row number instead.

This analysis is usually used with hundreds or thousands of P values, but can be done with any number.  

3. Choose the analysis

Click Analyze, look in the list of Column analyses, and choose Analyze a stack of P values.

 

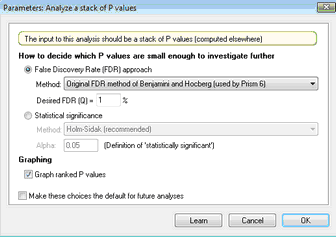
Choose one of two general approaches: Control the False Discovery Rate (FDR) or control the Type I error rate for the family of comparisons. Then choose the actual method you want Prism to use.

Control the False Discovery Rate (FDR)

Choose one of three approaches to decide which P values are small enough to flag as "discoveries". We recommend the adaptive method of Benjamini, Krieger and Yekutieli (1), as it has more power. The original FDR method of Benjamini and Hochberg (2) is better known, but has less power. The method of Benjamini and Yekutieli makes fewer assumptions, but has much less power.

Also set the value of Q, with the goal that no more than Q% of the comparisons flagged as discoveries, are false discoveries (false positives). Enter a percentage, not a fraction. If you want at most 5% of discoveries to be false, enter "5" not "0.05" and not "5%". There really is no standard value. If you enter a larger value, more comparisons will be flagged as discoveries, but more of these will be false discoveries.

Statistical significance (control Type I error rate for the family of comparisons)

Choose how Prism will correct for multiple comparisons. We recommend using the Holm-Šídák method, which has the most power. The alternatives are the methods of Bonferroni-Dunn or Bonferroni-Šídák.  The method we call Bonferroni-Dunn is often referred to simply as Bonferroni. The method we call Bonferroni-Šídák is often referred to simply as Šídák. The two are very similar. The Bonferroni-Šídák method has a bit more power but is less widely understood.

Set the value of alpha that applies to the entire family of P values. Prism then decides which P values are small enough for the related comparison to be designated "statistically significant" after correcting for multiple comparisons. Enter a fraction, not a percentage.  If you want 5% of comparisons under the null hypothesis to be falsely flagged as "significant", enter 0.05 not 5. If you enter a larger value, more comparisons will be flagged as "significant", but more of these will be false positives. For statistical significance, alpha is often set to 0.05 when making one or a few comparisons. But when making many comparisons, you'll probably want to enter a higher value.

Graphing

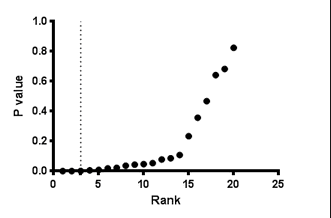
Check the option if you want to see a graph of P value rank vs. P value. This is a common way to visualize the distribution of P values.

References

1.Benjamini, Y., Krieger, A. M. & Yekutieli, D. Adaptive linear step-up procedures that control the false discovery rate. Biometrika 93, 491–507 (2006).

2.Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. Series B (Methodological) 289–300 (1995).

3.Benjamini, Y., & Yekutieli, D. (2001). The control of the false discovery rate in multiple testing under dependency. Annals of statistics, 1165–1188.