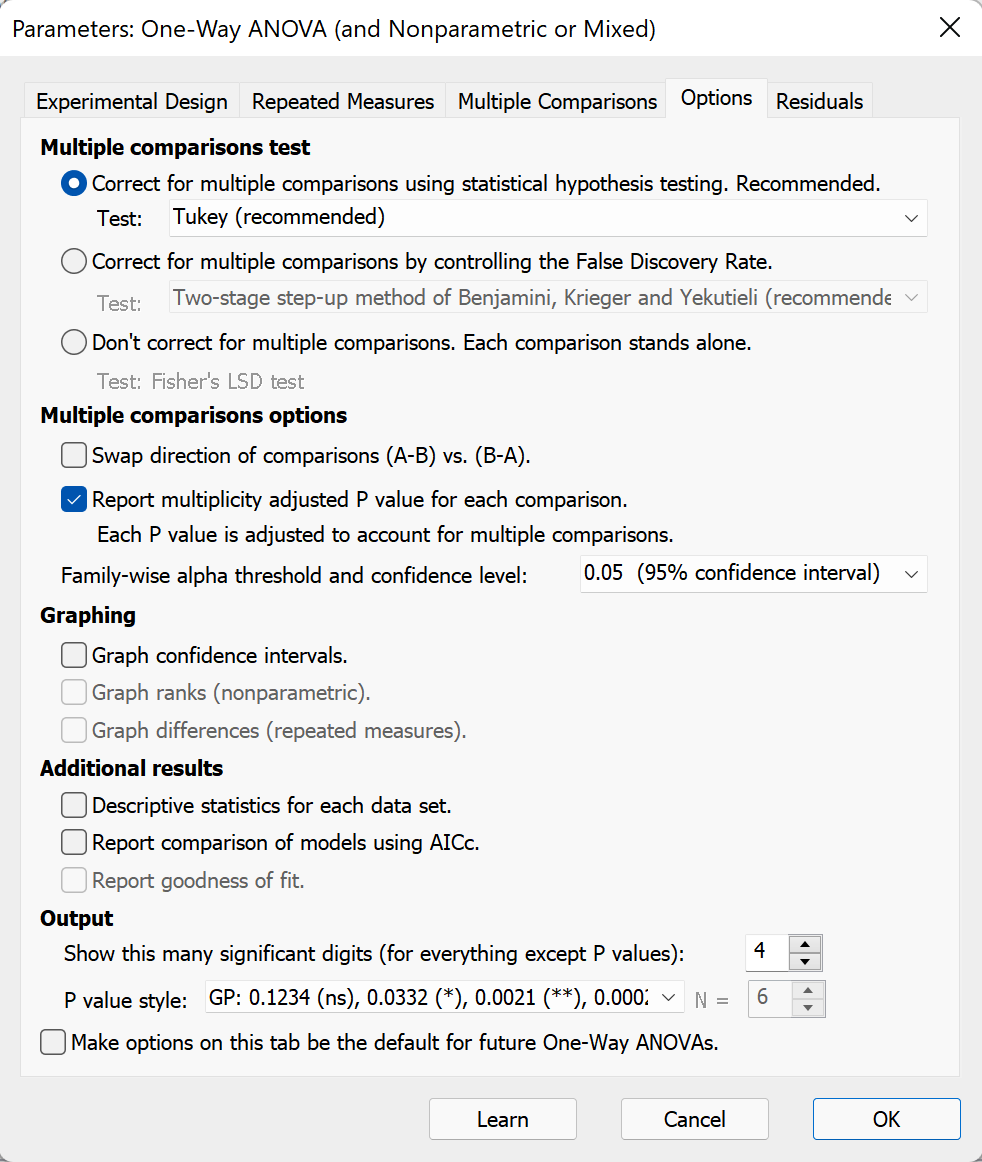
There are two help screens for the Options tab for the one-way ANOVA dialog:
•This page explains the multiple comparisons options.
•A different page explains the graphing and output options.
Which multiple comparison test?
First, choose the approach for doing the multiple comparisons testing
•Correct for multiple comparisons using statistical hypothesis testing.
•Correct for multiple comparisons by controlling the False Discovery Rate.
•Don’t correct for multiple comparisons. Each comparison stands alone.
If you aren’t sure which approach to use, Prism defaults to the first choice for three reasons:
•It is most conventional
•The results include actual multiplicity adjusted P values, rather than whether P is less than some threshold or whether a difference is a “discovery”
•Most tests in this category report confidence intervals (which we think is the best way to understand the results)
Once you’ve chosen an approach, choose the test. The choices depend on the goal you specified on the Multiple Comparisons (second) tab and whether or not you chose to assume equal SDs on the Experimental Design (first) tab.
Correct for multiple comparisons using statistical hypothesis testing
Compare every mean with every other mean
The available choices depend on whether you assume homoscedasticity (equal SDs, so equal variances) on the first tab of the ANOVA dialog.
If you assume homoscedasticity (equal SDs), you choices are:
•Tukey test (recommended)
•Holm-Sidak. This test is more powerful than the Tukey method (3), which means that it can sometimes find a statistically significant difference where the Tukey method cannot. This test cannot compute confidence intervals, and for this reason we prefer the Tukey test
•Newman-Keuls. We offer this test only for compatibility with old versions of Prism and other programs, but we suggest you avoid it. The problem is that it does not maintain the family-wise error rate at the specified level (1). In some cases, the chance of a Type I error can be greater than the alpha level you specified
If you do not assume homoscedasticity (equal SDs), your choices are:
•Games-Howell (recommended for large samples)
•Dunnett T3 (recommended when sample size per group is less than 50)
•Tamhane T2
All three methods can compute confidence intervals and multiplicity adjusted P values.
Compare a control mean with the other means
If you assume homoscedasticity (equal SDs), your choices are:
•Dunnett's (recommended)
•Holm-Sidak. Glantz says that Holm's test ought to have more power than Dunnett's test, but this has not (to his knowledge) been explored in depth(2). This test cannot compute confidence intervals or multiplicity adjusted P values, and for this reason we prefer the Dunnett test
If you do not assume homoscedasticity (equal SDs), your choices are:
•Dunnett's T3 (recommended)
Compare the means of prespecified pairs of columns
If you assume homoscedasticity (equal SDs), your choices are:
•Bonferroni (most commonly used)
•Sidak (more power, so recommended)
•Holm-Sidak (cannot compute confidence intervals)
If you do not assume homoscedasticity (equal SDs), your choices are:
•Games-Howell (recommended)
•Dunnett T3
•Tamhane T2
Correct for multiple comparisons by controlling the False Discovery Rate
Prism offers three methods to control the false discovery rate. All decide which (if any) comparisons to label as "discoveries" and do so in a way that controls the false discovery rate to be less than a value Q you enter.
The FDR approach is not often used as a followup test to ANOVA, but there is no good reason for that. This approach can categorize comparison as a “discovery” or not, but does not compute P values or confidence intervals.
Don't correct for multiple comparisons. Each comparison stands alone.
If you choose this approach, Prism will perform Fisher's Least Significant Difference (LSD) test.
This approach (Fisher's LSD) has much more power to detect differences. But it is more likely to falsely conclude that a difference is statistically significant. When you correct for multiple comparisons (which Fisher's LSD does not do), the significance threshold (usually 5% or 0.05) applies to the entire family of comparisons. With Fisher's LSD, that threshold applies separately to each comparison.
Only use the Fisher's LSD approach if you have a very good reason, and are careful to explain what you did when you report the results.
Multiple comparisons options
Swap direction of comparisons
The only effect of this option is to change the sign of all reported differences between means. A difference of 2.3 will be -2.3 if the option is checked. A difference of -3.4 will be 3.4 if you check the option. It is purely a personal preference that depends on how you think about the data.
Report multiplicity adjusted P value for each comparison
If you choose the Bonferroni, Tukey or Dunnett multiple comparisons test, Prism can also report multiplicity adjusted P values. If you check this option, Prism reports an adjusted P value for each comparison. These calculations take into account not only the two groups being compared, but the total number groups (data set columns) in the ANOVA, and the data in all the groups. With Dunnett's test, Prism can only report a multiplicity adjusted P value when it would be greater than 0.0001. Otherwise it reports "<0.0001" (prior to Prism 8, Prism reported 0.0001 without the less-than symbol).
The multiplicity adjusted P value is the smallest significance threshold (alpha) for the entire family of comparisons at which a particular comparison would be (just barely) declared to be "statistically significant".
Until recently, multiplicity adjusted P values have not been commonly reported. If you choose to ask Prism to compute these values, take the time to be sure you understand what they mean. If you include these values in publications or presentations, be sure to explain what they are.
Confidence and significance level (or desired FDR)
By tradition, confidence intervals are computed for 95% confidence and statistical significance is defined using an alpha of 0.05. Prism lets you choose other values. If you choose to control the FDR, select a value for Q (in percent). If you set Q to 5%, you expect up to 5% of the "discoveries" to be false positives.
The next page explains the graphing and output options.
References
1.SA Glantz, Primer of Biostatistics, sixth edition, ISBN= 978-0071435093.
2.MA Seaman, JR Levin and RC Serlin, Psychological Bulletin 110:577-586, 1991.