When performing a Kaplan-Meier survival analysis with more than two groups in Prism, you can choose to include multiple comparisons to assess pairs of groups. This feature is available beginning in Prism 10.5, and options for this feature are provided on the Multiple Comparisons tab of the survival analysis dialog.

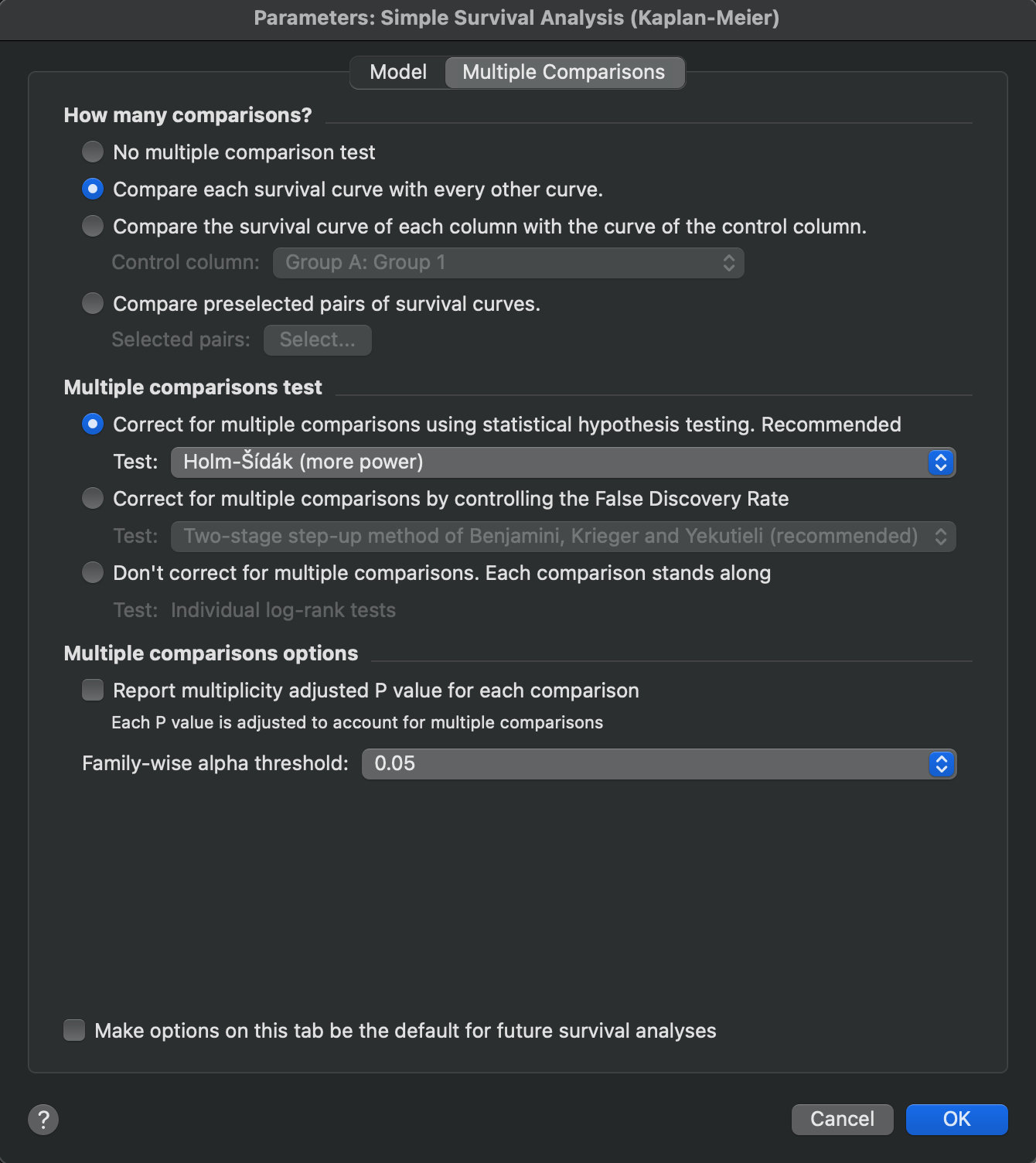
How many comparisons

These controls allow you to specify precisely which pairwise comparisons you would like Prism to perform. Choose between:

•No multiple comparison test - no comparisons will be performed

•Compare each survival curve with every other curve - this performs a comparison test on every possible combination of groups in the survival analysis. With three groups (A, B, and C), there are three possible comparisons (A vs B, A vs C, and B vs C). With four groups, there are six combinations; with five groups there are 10 combinations, and so on.

•Compare the survival curve of each column with the curve of a control column - this performs separate comparisons for a single control group against every other group. The number of comparisons made will be equal to the number of groups minus one (5 groups results in 4 comparisons, 3 groups results in 2 comparisons, etc.).

•Compare preselected pairs of survival curves - This option will allow you to specify the individual comparisons to be made. ONLY these comparisons will be performed and ONLY these comparisons will be considered when applying corrections for multiple comparisons. Be honest with yourself about how many comparisons you actually want to make. By selecting specific comparisons only after seeing the data, you're likely not applying the correction method appropriately. The following section discusses this in a bit more detail

How many comparisons are you really making?

You must be honest about the number of comparisons you are making. Say there are four treatment groups (including control group A). You then go back and compare the group with the longest survival with the group with the shortest survival. It is not fair to say that you are only making one comparison, since you couldn't decide which comparison to make without looking at all the data. With four groups, there are six pairwise comparisons you could make:

1.A vs B

2.A vs C

3.A vs D

4.B vs C

5.B vs D

6.C vs D

By looking at the data and selecting the shortest and longest curves, you have implicitly made all these comparisons, and so you must appropriately correct the results accordingly.

On the other hand, if you knew prior to conducting the experiment that you were only interested in comparing each of three treatment groups to the control group, and you weren't interested in comparing the treatments to each other, then you would be making three comparisons:

1.A vs B

2.A vs C

3.A vs D

Multiple comparisons test

Prism offers three different methods for handling correction of multiple comparisons tests:

1.Correct for multiple comparisons using statistical hypothesis testing

2.Correct for multiple comparisons by controlling the False Discovery Rate (FDR)

3.Don't correct for multiple comparisons. Each comparison stands alone

Prism's default is to use statistical hypothesis testing.

Statistical hypothesis testing method

This approach first performs all of the specified comparisons and determines their individual P values. It then uses the number of comparisons that were made along with the specified correction method, and adjusts the individual P values to ensure that the family-wise error rate (alpha) remains at the specified value. The net result of this correction method is that the adjusted P values are larger than their uncorrected counterparts to maintain the specified value of alpha. Prism offers three correction methods for adjusting multiple comparisons with statistical hypothesis testing following survival analysis:

1.Holm-Šídák - this test is the default for correcting multiple comparisons following survival analysis in Prism. It generally has more power than the other options

2.Bonferroni

3.Šídák

False discovery rate method

The false discovery rate method takes a different approach from the statistical hypothesis testing method. Rather than increasing the threshold to declare a result "statistically significant" (by decreasing alpha or equivalently increasing the individual P values), the FDR method controls the false-positive rate. Another way to say this is that this method ensures that - of the results which are identified as "discoveries" - less than a specified percentage of them will be false discoveries. This percentage is called the false discovery rate (indicated by Q) and is specified when performing the analysis.

Prism offers three methods to control the false discovery rate. All decide which (if any) comparisons to label as "discoveries" and do so in a way that controls the false discovery rate to be less than a value Q you specify.

1.Two-stage step-up method of Benjamini, Krieger and Yekutieli (recommended)

2.Original FDR method of Benjamini and Hochberg

3.Corrected method of Benjamini and Yekutieli (low power)

No correction

If you choose this option, Prism will simply perform individual (separate) log-rank tests on each of the specified pairwise comparisons. No correction will be made to any of the results. Choosing this method means that it's more likely to falsely determine that a comparison is "statistically significant". We recommend not using this option unless you have very good reasons to do so.

Multiple comparisons options

This section allows you to specify options related to the multiple comparisons correction method you selected for the analysis. If using a statistical hypothesis testing method to correct the multiple comparisons, you will have the option to report multiplicity adjusted P values for each comparisons. You will additionally be able to specify the family-wise alpha threshold to use for the family of comparisons being made. If you choose to apply no correction method, this value of alpha will apply to each individual comparison (each family will consist of a single comparison rather than a single family consisting of all comparisons being made).

If you choose to perform corrections with the false discovery rate method, you will be able to specify the desired value of Q.