Straight lines on graphs with logarithmic axes
The nonlinear regression analysis fits the data, not the graph. Since Prism lets you choose logarithmic axes, some graphs with data points that form a straight line follow nonlinear relationships. Prism's collection of "Lines" equations includes those that let you fit nonlinear models to graphs that appear linear when the X axis is logarithmic, the Y axis is logarithmic, or both axes are logarithmic. In these cases, linear regression will fit a straight line to the data but the graph will appear curved since an axis (or both axes) are not linear. In contrast, nonlinear regression to an appropriate nonlinear model will create a curve that appears straight on these axes.
Entering and fitting data
1.Create an XY table, and enter your X and Y values.
2.Go to the graph, double click on an axis to bring up the Format Axis dialog. Change one or both axes to a logarithmic scale. 
3.Click Analyze, choose Nonlinear regression (not Linear regression) and then choose one of the semi-log or log-log equations from the "Lines" section of equations.
Equations
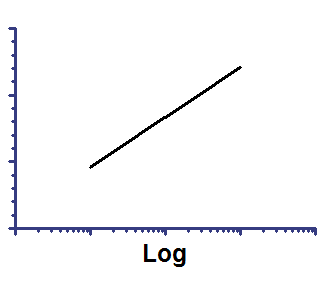
Semilog line -- X axis is logarithmic, Y axis is linear
Y=Yintercept + Slope*log(X)
On semilog axis |
On linear axes |
|
|
Slope is the change in Y when the log(X) changes by 1.0 (so X changes by a factor of 10).
Yintercept is the Y value when log(X) equals 0.0. So it is the Y value when X equals 1.0.
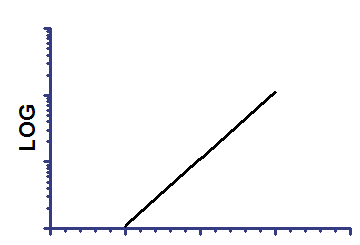
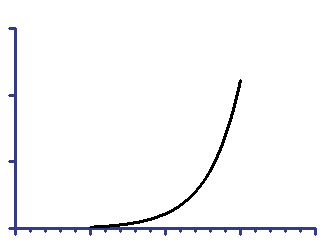
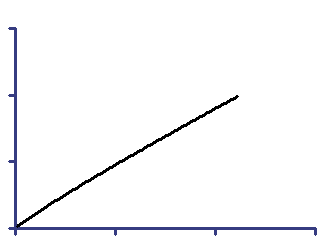
Semilog line -- X axis is linear, Y axis is logarithmic
Y=10^(Slope*X + Yintercept)
On semilog axis |
On linear axes |
|
|
Slope is the change in log(Y) when the X changes by 1.0.
Yintercept is the log(Y) value when X equals 0.0.
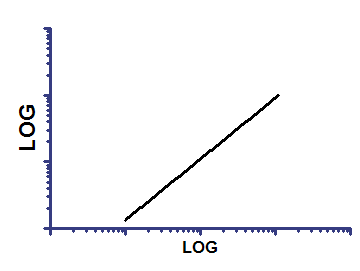
Log-log line -- Both X and Y axes are logarithmic
Y = 10^(slope*log(X) + Yintercept)
On log-log axes |
On linear axes |
|
|
Since both axes are transformed the same way, the graph is linear on both sets of axes. But when you fit the data, the two fits will not be quite identical.
Slope is the change in log(Y) when the log(X) changes by 1.0.
Yintercept is the Y value when log(X) equals 0.0. So it is the Y value when X equals 1.0.
An alternative way to handle these data
The nonlinear regression analysis minimizes the sum of the squares of the difference between the actual Y value and the Y value predicted by the curve. This is not the same as minimizing the sum of squares of the distances (as seen on the graph) between points and curve. In the graph below, the two vertical lines look the same distance but one represents a difference of 9 Y units, and the other a difference of 900.
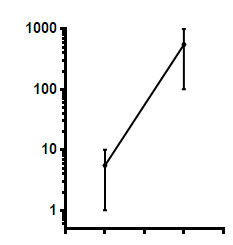
An alternative approach, that might be better in some circumstances, is to use Prism's transform analysis to transform Y (and maybe also X) to logarithms. Then perform linear regression on the logarithms. The regression results will not be the same as using nonlinear regression on log axes.