|
Advice: Don't compute the power to detect the difference actually observed |
Scroll Prev Top Next More |
Post-hoc power analyses are rarely useful
Some programs report a power value as part of the results of t tests and other statistical comparisons. Prism does not do so, and this page explains why.
It is never possible to answer the question "what is the power of this experimental design?". That question is simply meaningless. Rather, you must ask "what is the power of this experimental design to detect an effect of a specified size?". The effect size might be a difference between two means, a relative risk, or some other measure of treatment effect.
Which effect size should you calculate power for? How large a difference should you be looking for? These are not statistical questions, but rather scientific questions. It only makes sense to do a power analysis when you think about the data scientifically. It makes sense to compute the power of a study design to detect an effect that is the smallest effect you'd care about. Or it makes sense to compute the power of a study to find an effect size determined by a prior study.
When computing statistical comparisons, some programs augment their results by reporting the power to detect the effect size (or difference, relative risk, etc.) actually observed in that particular experiment. The result is sometimes called observed power, and the procedure is sometimes called a post-hoc power analysis or retrospective power analysis.
Many (perhaps most) statisticians (and I agree) think that these computations are useless and misleading. If your study reached a conclusion that the difference is not statistically significant, then -- by definition-- its power to detect the effect actually observed is very low. You learn nothing new by such a calculation. It can be useful to compute the power of the study to detect a difference that would have been scientifically or clinically worth detecting. It is not worthwhile to compute the power of the study to detect the difference (or effect) actually observed.
Observed power is directly related to P value
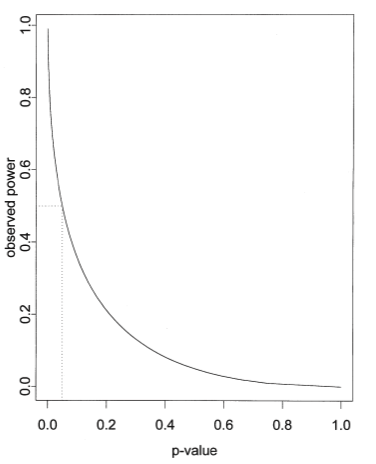
Hoenig and Helsey (2001) pointed out that the observed power can be computed from the observed P value as well as the value of alpha you choose (usually 0.05). When the P value is 0.05 (assuming you define statistical significance to mean P<0.05, so have set alpha to 0.05), then the power must be 50%. If the P value is smaller than 0.05, the observed power is greater than 50%. If the P value is greater than 0.05, then the observed power is less than 50%. The observed power conveys no new information. The figure below (from Helsey, 2001) shows the relationship between P value and observed power of an unpaired t test, when alpha is set to 0.05.
References
SN Goodman and JA Berlin, The Use of Predicted Confidence Intervals When Planning Experiments and the Misuse of Power When Interpreting the Results, Annals Internal Medicine 121: 200-206, 1994.
Hoenig JM, Heisey DM, 1710, The abuse of power, The American Statistician. February 1, 2001, 55(1): 19-24. doi:10.1198/000313001300339897.
Lenth, R. V. (2001), Some Practical Guidelines for Effective Sample Size Determination, The American Statistician, 55, 187-193
M Levine and MHH Ensom, Post Hoc Power Analysis: An Idea Whose Time Has Passed, Pharmacotherapy 21:405-409, 2001.
Thomas, L, Retrospective Power Analysis, Conservation Biology Vol. 11 (1997), No. 1, pages 276-280