What is a false minimum?
The nonlinear regression procedure adjusts the variables in small steps in order to improve the goodness-of-fit. If Prism converges on an answer, you can be sure that altering any of the variables a little bit will make the fit worse. But it is theoretically possible that large changes in the variables might lead to a much better goodness-of-fit. Thus the curve that Prism decides is the "best" may really not be the best.
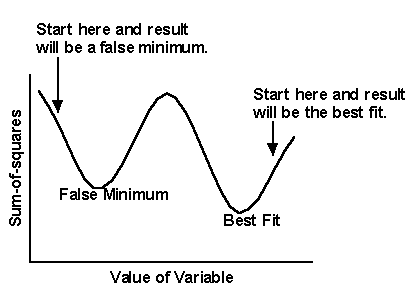
Think of latitude and longitude as representing two variables Prism is trying to fit. Now think of altitude as the sum-of-squares. Nonlinear regression works iteratively to reduce the sum-of-squares. This is like walking downhill to find the bottom of the valley. When nonlinear regression has converged, changing any variable increases the sum-of-squares. When you are at the bottom of the valley, every direction leads uphill. But there may be a much deeper valley over the ridge that you are unaware of. In nonlinear regression, large changes in variables might decrease the sum-of-squares.
This problem (called finding a local minimum) is intrinsic to nonlinear regression, no matter what program you use. You will rarely encounter a local minimum if your data have little scatter, you collected data over an appropriate range of X values, and you have chosen an appropriate equation.
Testing for a false minimum
To test for the presence of a false minimum:
1.Note the values of the variables and the sum-of-squares from the first fit.
2.Make a large change to the initial values of one or more parameters and run the fit again.
3.Repeat step 2 several times.
Ideally, Prism will report nearly the same sum-of-squares and same parameters regardless of the initial values. If the values are different, accept the ones with the lowest sum-of-squares.