This equation is used when X values are logarithms of doses or concentrations. Use a related equation when X values are concentrations or doses.
Introduction
Some drugs may cause an inhibitory response at low concentrations, and a stimulatory response at high concentrations, or vice-versa. The net result is a bell-shaped dose-response curve.
The model explained here is the sum of two dose-response curves, one that stimulates and one that inhibits. you will need lots of data to determine all the parameters without ambiguity, so this model will rarely be useful for data analysis. But it might be useful as a way to draw a smooth curve through the data
Step by step
Create an XY data table. Enter the logarithm of the concentration of the agonist into X. Enter response into Y in any convenient units.
From the data table, click Analyze, choose nonlinear regression, and choose the panel of equations: Dose-Response -- Special, X is log(concentration). Then choose Bell-shaped dose-response, X is log(concentration).
Consider constraining nH1 and nH2 to constant values of 1.0 (stimulation) and -1 (inhibition).
Model
Span1=Plateau1-Dip
Span2=Plateau2-Dip
Section1=Span1/(1+10^((LogEC50_1-X)*nH1))
Section2=Span2/(1+10^((X-LogEC50_2)*nH2))
Y=Dip+Section1+Section2
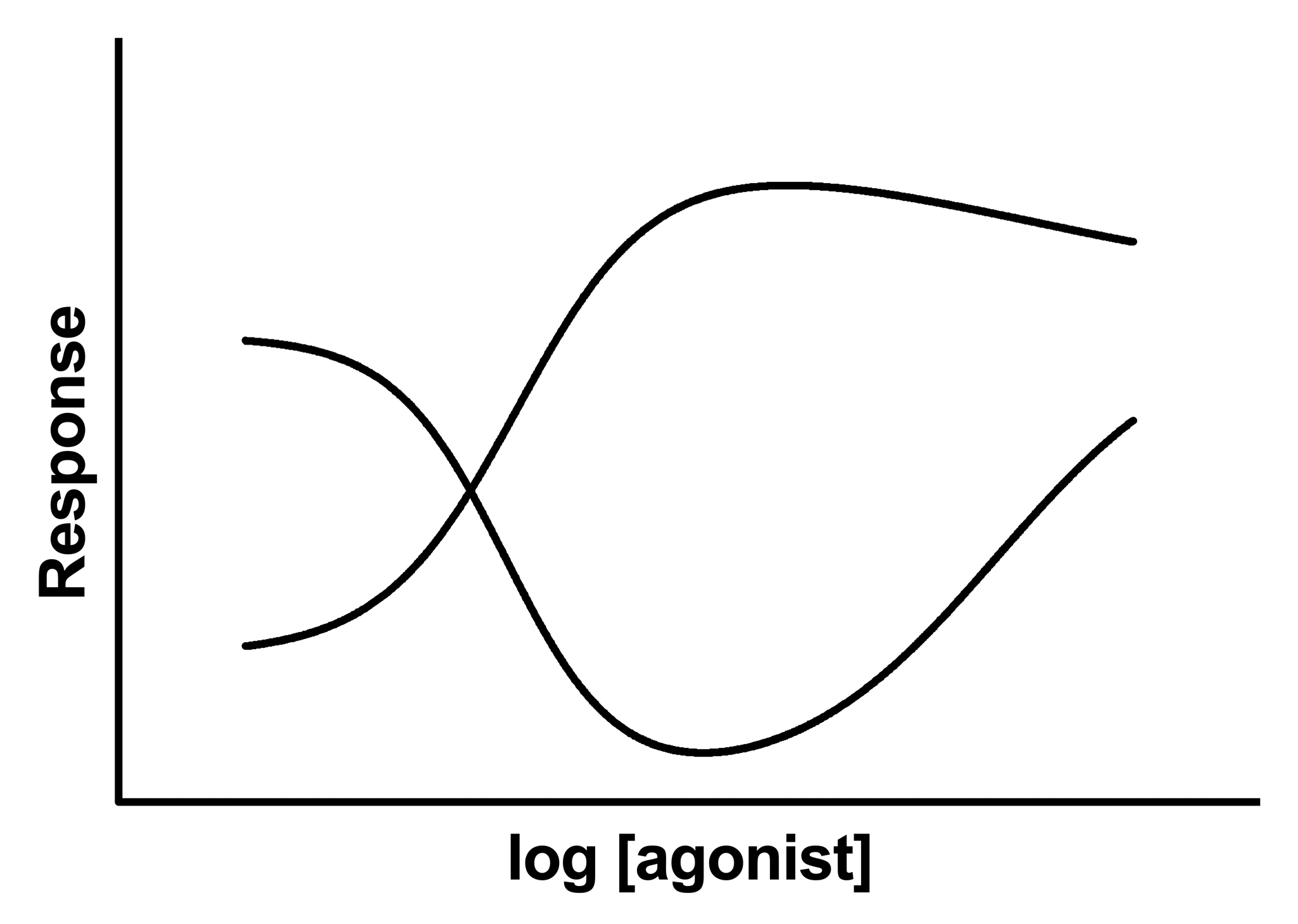
Interpret the parameters
Plateau1 and Plateau2 are the plateaus at the left and right ends of the curve, in the same units as Y.
Dip is the plateau level in the middle of the curve, in same units as Y. Note that when the curve goes up first (then down), this parameter named Dip would better be named Peak.
LogEC50_1 and LogEC50_2 are the concentrations that give half-maximal stimulatory and inhibitory effects in the same units as X.
nH1 and nH2 are the unitless slope factors or Hill slopes. Consider constraining these to equal 1.0 (stimulation) and -1 (inhibition).