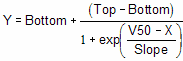
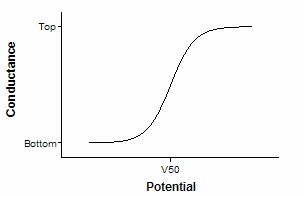
This equation describes voltage dependent activation of ion channels. It describes conductance (Y) as a function of the membrane potential (X). Conductance varies from BOTTOM to TOP. V50 is the potential at which conductance is halfway between BOTTOM and TOP. SLOPE describes the steepness of the curve, with a larger value denoting a shallow curve. Slope is expressed in units of potential, usually mV, and is positive for channels that activate upon depolarization.
Under appropriate experimental conditions, you can use SLOPE to calculate the valence (charge) of the ion moving across the channel. SLOPE equals RT/zF where R is the universal gas constant, T is temperature in °K, F is the Faraday constant, and z is the valence. Since RT/F » -26 mV at 25°C, z = -26/SLOPE.
BOTTOM is commonly made a constant equal to 0.0. If you also make TOP a constant equal to 1.0, then Y can be viewed as the fraction of channels that are activated.