Introduction
A competitive inhibitor reversibly binds to the same site as the substrate, so its inhibition can be entirely overcome by using a very high concentration of substrate. The Vmax doesn't change, and the effective Km increases. You can determine the Ki of a competitive inhibitor by measuring substrate-velocity curves in the presence of several concentrations of inhibitor.
Step by step
Create an XY data table. Enter substrate concentration into the X column, and enzyme activity into the Y columns. Each data set (Y column) represents data collected in the presence of a different concentration of inhibitor, starting at zero. Enter these concentrations into the column titles. Be sure to enter concentrations, not logarithms of concentration.
Alternatively, choose the competitive enzyme inhibition sample data set.
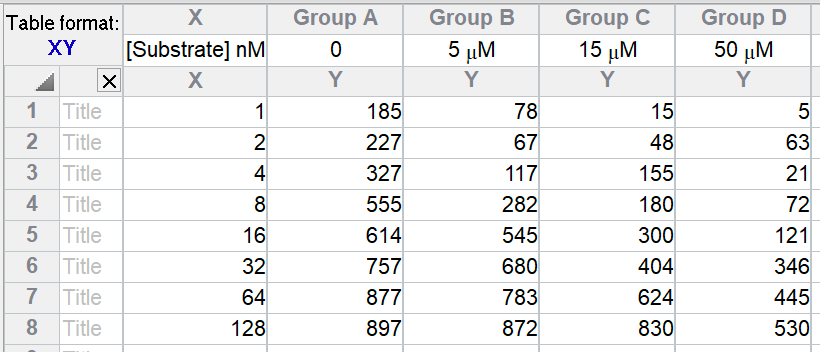
After entering data, click Analyze, choose nonlinear regression, choose the panel of enzyme kinetics equations, and choose Competitive enzyme inhibition.
The model
KmObs=Km*(1+[I]/Ki)
Y=Vmax*X/(KmObs+X)
The constant I is the concentration of inhibitor, a value you enter into each column title. This is constrained to equal a data set constant.
The parameters Vmax, Km and Ki are shared, so Prism fits one best-fit value for the entire set of data.
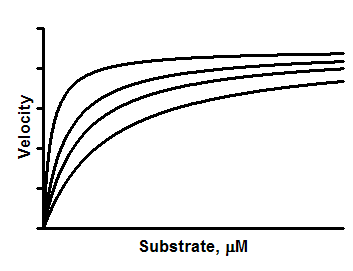
Interpreting the parameters
Ki is the inhibition constant, expressed in the same units as I, which you entered into the column titles.
Vmax is the maximum enzyme velocity, in the absence of inhibitor, expressed in the same units as Y.
Km is the Michaelis-Menten constant, expressed in the same units as X. It describes the interaction of substrate and enzyme in the absence of inhibitor.
If the data don't fit the model well, consider instead fitting to a noncompetitive or uncompetitive model. Or fit to the more general equation for mixed-model inhibition.
Reference
Equation 3.1 in: RA Copeland, Evaluation of Enzyme Inhibitors in Drug Discovery, Wiley 2005. IBSN:0471686964.RA Copeland, Evaluation of Enzyme Inhibitors in Drug Discovery, Wiley 2005. IBSN:0471686964.