This equation is used when X values are logarithms of doses or concentrations. Use a related equation when X values are concentrations or doses.
Introduction
A competitive inhibitor competes for agonist binding to a receptor, and shifts the dose-response curve to the right without changing the maximum response. This model fits two dose response curves and determines the fold shift.
Step by step
1.Create an XY data table.
2.Enter the logarithm of the concentration of the agonist ligand into the X column.
3.Enter response into Y in any convenient units. Enter data with no inhibitor into column A. Enter data collected with a constant concentration of inhibitor into column B. You can label columns A and B with any column title you like. The column title does not get used as part of the analysis.
4.From the data table, click Analyze, choose nonlinear regression, and choose the panel of equations: Dose-Response -- Special, X is log(concentration). Then choose EC50 shift, X is log(concentration).
5.If you have subtracted off any baseline signal, constrain the parameter Bottom to a constant value of zero.
Model
<A>LogEC=LogEC50Control
<~A>LogEC=LogEC50Control + log(EC50Ratio)
Y=Bottom + (Top-Bottom)/(1+10^((LogEC-X)*HillSlope))
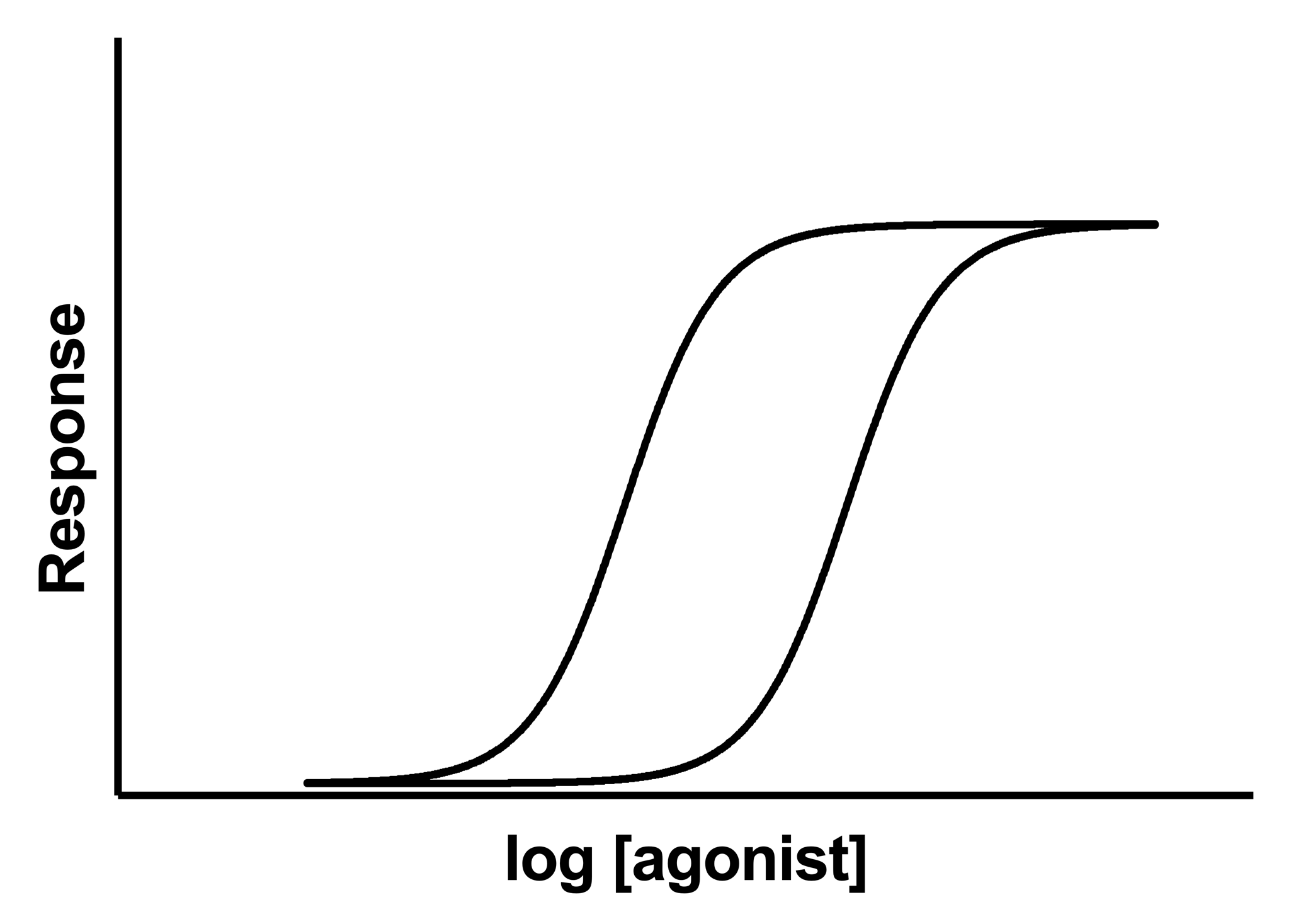
EC50Control is the concentration of agonist that gives half maximal response in the absence of modulator.
Top and Bottom are plateaus in the units of the Y axis (shared).
EC50Ratio is the ratio of EC50 in presence of inhibitor divided by EC50 of agonist alone.
HillSlope is the slope factor (shared)
Notes
•If you have several concentrations of antagonist, use a different model that will directly fit the Schild model (using either X as concentration of agonist or X as the logarithm of the concentration of agonist) and determine the pA2.
•If you want to test the null hypothesis that the EC50 ratio is 1.0 (no shift), that is easy to do. Go to the Compare tab, choose to test whether a selected parameter differs from a hypothetical value, choose the parameter EC50Ratio, and enter the hypothetical value 1.0.
•This model shares Top, Bottom and HillSlope. So it assumes that both models are exactly the same except (perhaps) for the EC50. You can go to the Constrain tab and lift this constraint for any or all of these three parameters, if you think it makes sense not to share them.