This equation is used when X values are concentrations or doses. Use a related equation when X values are logarithms of concentrations or doses.
Introduction
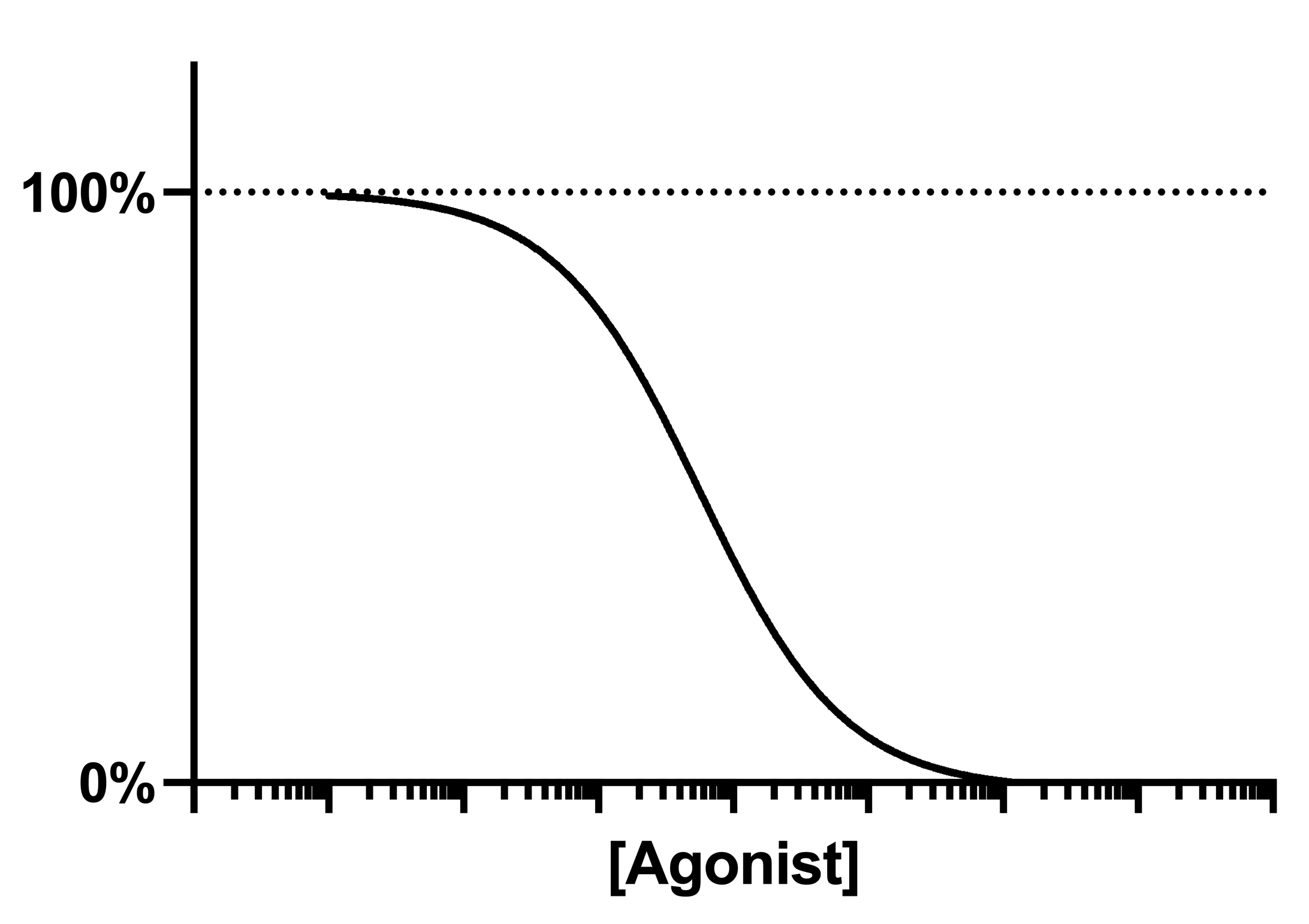
Many log(inhibitor) vs. response curves follow the familiar symmetrical sigmoidal shape.
If you have good control data, it can make sense to normalize the response to run between 0% and 100%. This model assumes that the data have been normalized, so forces the curve to run from 100% down to 0%. The goal is to determine the IC50 of the inhibitor - the concentration that provokes a response equal to 50%.
It only makes sense to fit a normalized model when you are sure you have defined 0% and 100% quite accurately. If your data define a complete sigmoidal curve, it is best to fit the entire curve and let Prism fit the Top and Bottom plateaus. If your data don't form a full sigmoidal curve, but you can define the bottom and top by solid control data, then fitting to a normalized model is preferable.
Many inhibitory dose-response curves have a standard slope of -1.0. This model does not assume a standard slope but rather fits the Hill Slope from the data, and so is called a Variable slope model. This is preferable when you have plenty of data points.
Step by step
Create an XY data table. Enter the concentrations of the inhibitor into X. Enter response into Y in any convenient units. Enter one data set into column A, and use columns B, C... for different treatments, if needed.
From the data table, click Analyze, choose nonlinear regression, choose the panel of equations "Dose-response curves - Inhibition" and then choose the equation "log(inhibitor) vs. normalized response -- variable slope".
Since the uncertainty of the EC50 is very asymmetric, be sure to choose to compute the confidence intervals using the likelihood ratio asymmetric method.
Double click on the X axis of the graph, and choose (at the upper left of the Format Graph dialog) to stretch the axis to a logarithmic scale.
Model
Y=100/(1+(IC50/X)^HillSlope)
Interpret the parameters
IC50 is the concentration of agonist that gives a response half way between Bottom and Top. This is not the same as the response at Y=50. Depending on which units Y is expressed in, and the values of Bottom and Top, the IC50 may give a response nowhere near "50". Prism reports both the IC50 and its log.
HillSlope describes the steepness of the family of curves. A HillSlope of -1.0 is standard, and you should consider constraining the Hill Slope to a constant value of -1.0. A Hill slope more negative than -1 (say -2) is steeper.