Introduction
This equation describes the growth with a constant doubling time.
Entering data
Create an XY data table. Enter time into X, and response (cell number ..) into Y. If you have several experimental conditions, place the first into column A, the second into column B, etc.
Note that Y values must be the actual values. If you transform all the values to logarithms, then it rarely would make sense to fit this equation.
After entering data, click Analyze, choose nonlinear regression, choose the panel of exponential equations, and choose Exponential growth.
Consider constraining Y0 to a constant value
The parameter Y0 is the Y value at time zero. In many cases, you will know this value precisely. If so, you should constrain that parameter to be a constant value. To do this, go to the Constrain tab of the nonlinear regression dialog, set the drop down next to Y0 to "Constant equal to" and enter its value.
Model
Y=Y0*exp(k*X)
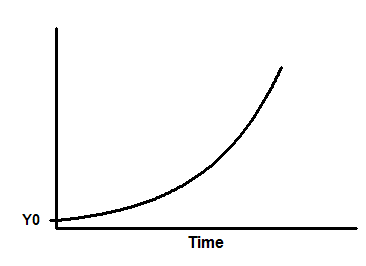
Y0 is the Y value when X (time) is zero. It is expressed in the same units as Y,
K is the rate constant, expressed in reciprocal of the X axis time units. If X is in minutes, then K is expressed in inverse minutes.
Tau is the time constant, expressed in the same units as the X axis. It is computed as the reciprocal of K.
Doubling-time is in the time units of the X axis. It is computed as ln(2)/K.
Consider fitting a line (linear regression) to transformed data
When you fit any model with nonlinear regression, you assume that the variation of residuals is Gaussian with the same SD all the way along the curve. With growth data, often the variation goes up as Y goes up. One way to deal with this is by weighting the data. Another approach would be to transform all the Y values to ln(Y) and fit linear regression to the results. The slope in linear regression will have the same meaning as K in the equation above.