1. Create a data table
From the Welcome or New Table dialog, choose to create XY data table.
If you are just getting started, choose the sample data: Linear regression -- Compare slopes.
If you are entering your own data, choose the subcolumn format. Choose replicate values if you have replicates to enter. Prism can plot error bars automatically. You can also choose to enter data where the mean and SD (or SEM) have already been calculated. In this case, if you want to take into account variations in the SD from point to point, use nonlinear regression to fit the line.
2. Enter data
If you chose sample data, you'll see these values:
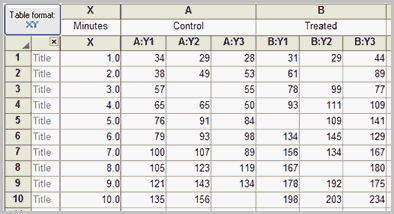
If you enter Y values for several data sets (column A, B and C), Prism will report regression results for X vs. YA, for X vs. YB, and for X vs. YC. It can also test whether the slopes (and intercepts) differ significantly.
If the different data sets don't share the same X values, use different rows for different data sets like this:
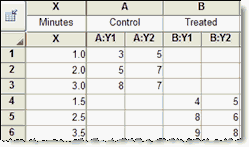
3. Analysis choices
Click Analyze, and then choose linear regression from the list of XY analyses.
Force the line to go through a specified point (such as the origin)?
If you choose regression, you may force the line to go through a particular point such as the origin. In this case, Prism will determine only the best-fit slope, as the intercept will be fixed. Use this option when scientific theory tells you that the line must go through a particular point (usually the origin, X=0, Y=0) and you only want to know the slope. This situation arises rarely.
Use common sense when making your decision. For example, consider a protein assay. You measure optical density (Y) for several known concentrations of protein in order to create a standard curve. You then want to interpolate unknown protein concentrations from that standard curve. When performing the assay, you adjusted the spectrophotometer so that it reads zero with zero protein. Therefore you might be tempted to force the regression line through the origin. But this constraint may result in a line that doesn't fit the data very well. Since you really care that the line fits the standards very well near the unknowns, you will probably get a better fit by not constraining the line.
If in doubt, you should let Prism find the best-fit line without any constraints.
Fit linear regression to individual replicates or to means?
If you collected replicate Y values at every value of X, there are two ways to calculate linear regression. You can treat each replicate as a separate point, or you can average the replicate Y values, to determine the mean Y value at each X, and do the linear regression calculations using the means.
You should consider each replicate a separate point when the sources of experimental error are the same for each data point. If one value happens to be a bit high, there is no reason to expect the other replicates to be high as well. The errors are independent.
Average the replicates and treat the mean as a single value when the replicates are not independent. For example, the replicates would not be independent if they represent triplicate measurements from the same animal, with a different animal used at each value of X (dose). If one animal happens to respond more than the others, that will affect all the replicates. The replicates are not independent.
Test departure from linearity with runs test
See Runs test
Test whether slope and intercept are significantly different
If you have entered data for two or more datasets, Prism can test whether the slopes differ significantly.
Confidence and prediction bands
Learn about confidence and prediction bands.