What is segmental regression?
In some situations you may wish to fit different models to different portions of your data. This is called segmental regression. This often occurs in kinetic experiments where you add a drug or perform some sort of intervention while recording data. The values collected before the intervention follow a different model than those collected afterwards.
If you didn't perform an intervention at a particular time along the X axis, it is unlikely that this kind of segmental regression is the analysis of choice.
How to perform segmental regression with Prism
Although Prism has no built-in way to fit different equations to different portions of the data, you can achieve that effect using a user-defined equation containing the IF function.
In this example, you collected data that established a baseline early in the experiment, up to "Start". You then added a drug, and followed the outcome (Y) as it increased towards a plateau. Prior to the injection, the data followed a horizontal line; after the injection the data formed an exponential association curve.
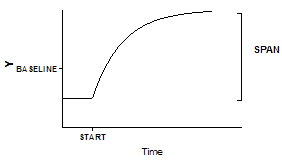
Y1=BASELINE
Y2=BASELINE + SPAN*(1-exp(-K*(X-START)))
Y=IF[(X<START),Y1,Y2)]
It is easiest to understand this equation by reading the bottom line first. For X values less than START, Y equals Y1, which is the baseline. Otherwise, Y equals Y2, which is defined by the exponential association equation.
This equation has two intermediate variables (Y1 and Y2). Prism can fit the four true variables: START, SPAN, K, and BASELINE.
In many cases, you will make START a constant equal to the time of the experimental intervention. If you want Prism to fit START, choose an initial value carefully.
This kind of model is most appropriate when X is time, and something happens at a particular time point to change the model. In the example above, a drug was injected at time=Start.
How to fit a model to only a portion of the data
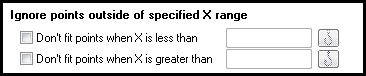
The Range tab of the nonlinear regression dialog lets you define an X range that determines which points are fit and which are ignored.