The extra-sum-of-squares F test compares nested models
The extra-sum-of-squares F test compares the goodness-of-fit of two alternative nested models. "Nested" means that one model is a simpler case of the other. Let's consider what this means in different contexts:
• If you asked Prism to test whether parameters are different between treatments, then the models are nested. You are comparing a model where Prism finds separate best-fit values for some parameters vs. a model where those parameters are shared among data sets. The second case (sharing) is a simpler version (fewer parameters) than the first case (individual parameters).
• If you asked Prism to test whether a parameter value is different than a hypothetical value, then the models are nested. You are comparing the fit of a model where a parameter is fixed to a hypothetical value to the fit of a model where Prism finds the best-fit value of that parameter. The first case (fixed value) is a simpler version (fewer parameters to fit) than the second.
•if you are comparing the fits of two equations you chose, and both models have the same number of parameters, then the two models cannot be nested. With nest models, one model has fewer parameters than the other. When the two models have the same number of parameters, Prism reports that it cannot compute the F test because the two models have the same number of degrees of freedom. In this case, Prism does not report a P value, and chooses to plot the model whose fit has the lower sum-of-squares. Prism reports the error message, "Models have the same DF."
•if you are comparing the fits of two equations you chose with different numbers of parameters, the models may or may not be nested. Prism does not attempt to do the algebra necessary to make this determination. If you chose two models that are not nested, Prism will report results for the extra-sum-of-squares F test, and these results will not be useful.
Interpreting the P value
The extra-sum-of-squares F test is based on traditional statistical hypothesis testing. The F test compares the improvement of SS with the more complicated model vs. the loss of degrees of freedom.
The null hypothesis is that the simpler model (the one with fewer parameters) is correct. The improvement of the more complicated model is quantified as the difference in sum-of-squares. You expect some improvement just by chance, and the amount you expect by chance is determined by the number of degrees of freedom in each model. The F test compares the difference in sum-of-squares with the difference you’d expect by chance. The result is expressed as the F ratio, from which a P value is calculated.
The P value answers this question:
If the null hypothesis is really correct, in what fraction of experiments (the size of yours) will the difference in sum-of-squares be as large as you observed, or even larger?
If the P value is small, conclude that the simple model (the null hypothesis) is wrong, and accept the more complicated model. Usually the threshold P value is set at its traditional value of 0.05.
If the P value is high, conclude that the data do not present a compelling reason to reject the simpler model.
Prism names the null and alternative hypotheses, and reports the P value. You set the threshold P value in the Compare tab of the nonlinear regression dialog. If the P value is less than that threshold, Prism chooses (and plots) the alternative (more complicated) model. It also reports the value of F and the numbers of degrees of freedom, but these will be useful only if you want to compare Prism's results with those of another program or hand calculations.
When Prism won't report a P value when comparing models
Prism skips the extra sum of squares test and does not report a P value in these situations:
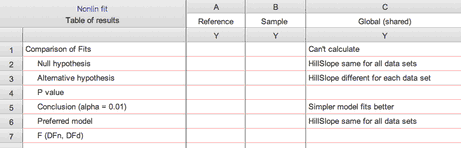
•If the simpler model fits the data better than (or the same) as the more complicated model. The whole point of the F test is to deal with a tradeoff. The model with more parameters fits the data better fit, but that may just be due to chance. The F test asks if that improvement in fit (decrease in sum of squares) is large enough to be "worth" the loss in degrees of freedom (increase in number of parameters). In the rare cases where the simpler model fits better (or the same) as the more complicated model (the one with more parameters), Prism will choose the simpler model without computing the F test and report "Simpler model fits better":
• If the fit of either model is ambiguous or flagged, then Prism chooses the other model without performing any statistical test. You have a choice in the Compare tab of nonlinear regression to turn off this criterion.
•If the fit of one model did not converge, then Prism chooses the other model without doing the F test. Since the fit of one model didn't converge, it makes no sense to compare the sum-of-squares of the two models.
•If one model fits the data perfectly, so the sum of squares equals zero. If one model fits perfectly, Prism chooses it without doing the F test.
•If the two models have the same number of degrees of freedom. The idea of the F test is to balance the improvement of sum-of-squares (better fit) with the decrease in degrees of freedom (more parameters). The F test makes no sense (and is mathematically impossible due to division by zero) if the two models have the same number of degrees of freedom. In this case, Prism picks the model that fits best.