Introduction
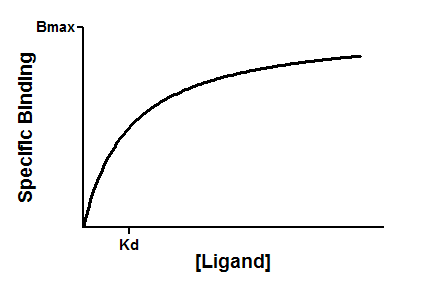
In a saturation binding experiment, you vary the concentration of radioligand and measure binding. The goal is to determine the Kd (ligand concentration that binds to half the receptor sites at equilibrium) and Bmax (maximum number of binding sites).
The ligand binds not only to receptors sites, but also to nonspecific sites. There are three approaches to dealing with nonspecific binding.
•Subtract off the nonspecific, and analyze only the specific binding. Read on for this approach.
•Analyze the total binding only, inferring the amount of nonspecific binding from the shape of the total binding curve. Learn more.
•Globally analyze the total and nonspecific binding at one time. Learn more.
Step by step
Create an XY data table. Enter radioligand concentration into X, and specific binding into Y. If you have several experimental conditions, place the first into column A, the second into column B, etc.
An alternative approach would be to enter total binding into column A, and nonspecific into column B. Then use the Remove Baseline analysis to subtract column B from column A, creating a new results table with the specific binding.
From the table of specific binding, click Analyze, choose nonlinear regression, choose the panel of Saturation Binding equations, and choose One site specific binding.
Model
Y = Bmax*X/(Kd + X)
Interpret the parameters
Bmax is the maximum specific binding in the same units as Y. It is the specific binding extrapolated to very high concentrations of radioligand, and so its value is almost always higher than any specific binding measured in your experiment.
Kd is the equilibrium dissociation constant, in the same units as X. It is the radioligand concentration needed to achieve a half-maximum binding at equilibrium.
Create a Scatchard plot
Before nonlinear regression was available, investigators had to transform curved data into straight lines, so they could analyze with linear regression. One way to do this is with a Scatchard plot, which plots specific binding vs. the ratio of specific binding to the concentration of free radioligand.

If you create a Scatcahrd plot, use it only to display your data. The human retina and visual cortex evolved to detect edges (straight lines), not rectangular hyperbolas, and so it can help to display data this way. Scatchard plots are often shown as insets to the saturation binding curves. They are especially useful when you want to show a change in Bmax or Kd.
Don't use the slope and intercept of a linear regression line to determine values for Bmax and Kd. If you do this, you won't get the most accurate values for Bmax and Kd. The problem is that the transformation distorts the experimental error, so the data on the Scatchard plot do not obey the assumptions of linear regression. Use nonlinear regression to obtain the most accurate values of Kd and Bmax.
To create a Scatchard plot from your specific binding data, use Prism's Transform analysis, and choose the Scatchard transform from the panel of biochemistry and pharmacology transforms.
To create a Scatchard line corresponding to the nonlinear regression fit, follow these steps:
1.Create a new XY data table, with no subcolumns.
2.Into row 1 enter X=0, Y=Bmax/Kd (previously determined by nonlinear regression).You need to do the calculation manually, and enter a number.
3.Into row 2 enter X=Bmax and Y=0. Again enter the number into the X column, not the text 'Bmax'.
4.Note the name of this data table. Perhaps rename it to something appropriate.
5.Go to the Scatchard graph.
6.Drag the new table from the navigator and drop onto the graph.
7.Double-click on one of the new symbols for that data set to bring up the Format Graph dialog.
8.Choose to plot no symbols, but to connect with a line.
Notes
•This is not the best way to determine Bmax and Kd. It is better to globally fit total and nonspecific binding, without subtracting to compute specific binding.
•When making a Scatchard plot, you have to choose what units you want to use for the Y-axis. Some investigators express both free ligand and specific binding in cpm so the ratio bound/free is a unitless fraction. While this is easy to interpret (it is the fraction of radioligand bound to receptors), an alternative is to express specific binding in sites/cell or fmol/mg protein, and to express the free radioligand concentration in nM. While this makes the Y-axis hard to interpret visually, it provides correct units for the slope (which equals -1/Kd).
•This equation is equivalent to the Langmuir isotherm for the absorption of a gas onto a surface.