This equation is used when X values are logarithms of doses or concentrations. Use a related equation when X values are concentrations or doses.

Introduction to the operational model

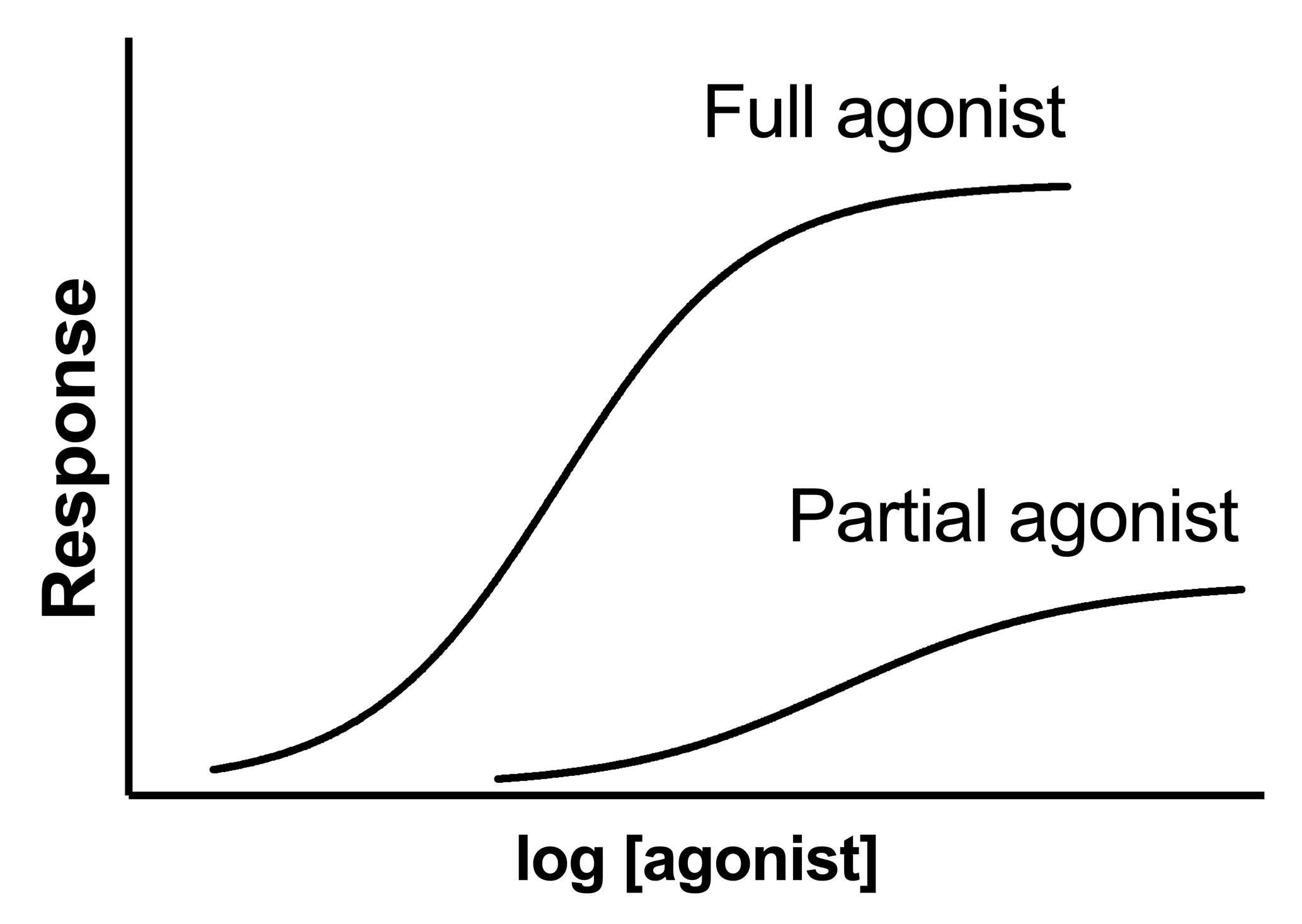
The EC50, fit by standard dose-response models, is determined by two properties of the agonist:

•How well it binds to the receptor, quantified by the affinity of the drug for binding to its receptor.

•How well it causes a response once bound. This property is known as the agonist’s efficacy. Since efficacy depends on both agonist and tissue, a single drug acting on a single kind of receptor can have different efficacies, and thus different EC50 values, in different tissues.

A single dose-response experiment cannot determine affinity and efficacy. A drug that binds tightly with high affinity but has low efficacy, will produce exactly the same dose-response curve as a drug with low affinity and high efficacy.

To determine the affinity of a partial agonist, use the operational model to globally fit the dose-response curves of both a full agonist and the partial agonist. The data from the full-agonist determines the maximum possible effect. Knowing that, the fitting can determine the affinity of the partial agonist.

Step by step

Create an XY data table. Enter the logarithm of the concentration of the agonist ligand into X. Enter response into Y in any convenient units. Enter data with the full agonist into column A. Enter data collected with a partial agonist into column B. Repeat, if you have data with different partial agonists, for column C, D, E, ..., each with a different amount of depletion.

From the data table, click Analyze, choose nonlinear regression, and choose the panel of equations:  Dose-Response -- Special, X is log(concentration). Then choose Operational Model - Partial agonist, X is log(concentration).

If you have subtracted off any basal response, consider constraining the parameter Basal to a constant value of zero.

Also consider constraining the transducer slope n to a constant value of 1.0. When set to 1.0, all dose-response curves are constrained to have Hill slopes of 1.0, which is observed commonly. If n is not 1.0, the Hill slopes will not be 1.0, but the Hill slopes will not equal exactly n.

Model

operate= (((10^logKA)+(10^X))/(10^(logtau+X)))^n

<A> Y = Basal + (Effectmax-Basal)/(1+10^((LogEC50-X)*n))

<~A> Y = Basal + (Effectmax-Basal)/(1+operate)

The second line is preceded with <A> which means it only applies to the first data set. It fits a variable slope dose-response curve. The third line is preceded with <~A> which means it applies to all data set except the first. It fits the operational model to determine the affinity (KA) of the partial agonist.

Interpret the parameters

Effectmax is the maximum possible system response, in units of the Y axis. It is the top plateau of the full agonist's dose-response curve.

Basal is the response in absence of agonist, in same units as Y. If you have subtracted off any basal response, constrain basal to a constant value of zero.

n is the Unitless transducer slope. It is similar to, but not identical to, the Hill slope. In most cases, n is constrained to a constant value of 1.0, in which case all the dose-response curves will have Hill slopes of 1.0. If n does not equal 1.0, the Hill Slope does not equal either 1.0 or n.

KA is the equilibrium dissociation constant of the partial agonist(s), in same units as X (usually molar). It measures the affinity of the partial agonist for the receptors, which is the main goal of this kind of experiment. Prism reports both KA and its logarithm. It is not the same as the EC50. By definition, it cannot be computed for the first data set (the full agonist).

tau is the transducer constant, a practical measure of efficacy. It is the inverse of the fraction of receptors that must be occupied by agonist to obtain the half-maximal response. If t equals 10, that means that occupation of only 10% of the receptors leads to a half-maximal response. If t equals 1.0, that means that it requires occupation of all the receptors to give a half-maximal response. This would happen with a partial agonist. Prism reports both tau and its logarithm, and fits tau individually for each data set.  By definition, it cannot be computed for the first data set (the full agonist).

Reference                                                                                                                      

Black and Leff (Proc. R. Soc. Lond. B, 220: 141-162, 1983