Introduction
An allosteric modulator can reduce radioligand binding. This model fits experiments, where entire radioligand binding curves are measured in the absence and presence of modulator. The goal is to learn the affinity of the modulator for binding to its site, and also determine the value of alpha, the ternary complex constant that quantifies the degree to which binding of the modulator alters the affinity of the radioligand for the receptor site.
Step by step
Create an XY data table. Enter the concentration of the labeled ligand into X, using any convenient units (maybe nM). Enter specific binding into Y in any convenient units. Enter data with no modulator into column A. Enter data collected with a constant concentration of modulator into column B. Repeat, if you have data, for column C, D, E, ..., each with a different concentration of modulator. Enter the modulator concentration (in nanomolar so 1nM is entered as '1') into the column titles. Don't forget to enter '0' as the column title for data set A.
From the data table, click Analyze, choose nonlinear regression, choose the panel of Saturation Binding equations, and choose Allosteric modulator shift.
You don't need to constrain any parameters to constant values.
Model
Hot=X
Alpha=10^logalpha
KB=10^logKB
KApp=KDHot*((1+Allo/KB)/(1+alpha*Allo/KB))
Y=Bmax*Hot/(Hot+KApp)
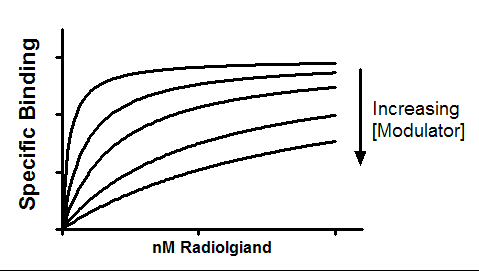
Interpret the parameters
Kb is the equilibrium dissociation constant (Molar) of modulator binding to its allosteric site. It is in the same molar units used to enter the modulator concentration into column titles on the data table.
KdHot is the equilibrium dissociation constant of the radioligand. It is expressed in the same units used to enter X values, nM in the example.
Alpha is the ternary complex constant. When alpha=1.0, the modulator won't alter binding. If alpha is less than 1.0, then the modulator reduces ligand binding. If alpha is greater than 1.0, then the modulator increases binding. In the example shown about, alpha equals 0.01 so the modulator greatly decreases binding.
Notes
•This model is designed to analyze data when the unlabeled compound works via an allosteric site. Since the labeled and unlabeled ligands are acting via different sites, it is inappropriate (and incorrect) to refer to the modulator as a competitor.
•The model is written to fit the logarithm of alpha, rather than alpha itself. This is because alpha is asymmetrically (all values from 0 to 1 mean that the modulator decreases binding, while all values from 1 to infinity mean that the modulator enhances binding. On a log scale, its values are more symmetrical, so the confidence interval computed on a log scale (as Prism does) are more accurate. Prism reports both alpha and log(alpha).
•This model assumes that the allosteric modulator is present in excess, so the concentration you added is very close to its free concentration. This model won't work when the concentration of allosteric modulator is limiting (as it is when G proteins alter agonist binding to many receptors). No explicit model can handle this situation. You need to define the model with an implicit equation (Y on both sides of the equals sign) and Prism cannot handle such equations.
Reference
A. Christopoulos and T. Kenakin, Pharmacol Rev, 54: 323-374, 2002