Prism provides best-fit values for β0 and β1 based off of maximum likelihood estimation. Remember that the form of the logistic model can be expressed in two equivalent forms:
Log(Odds) = β0 + β1*X, or
Logit(P(Y=1)) = β0 + β1*X
Because of the logit transformation, interpretation of the model coefficients is more difficult than with linear regression. β0 and β1 are, respectively, the slope and intercept of the model for the log odds of Y = 1. That’s a mouthful, and is difficult for most people to interpret. It is correct (although not particularly helpful to say), “For a 1 unit increase in X, the log odds increases by β1.” Instead, people usually interpret the coefficients using odds ratios as described in a later section. You can learn more about the relationship of probability, odds, and log odds here.
Prism reports both standard errors and (profile likelihood) confidence intervals for β0 and β1 estimates.
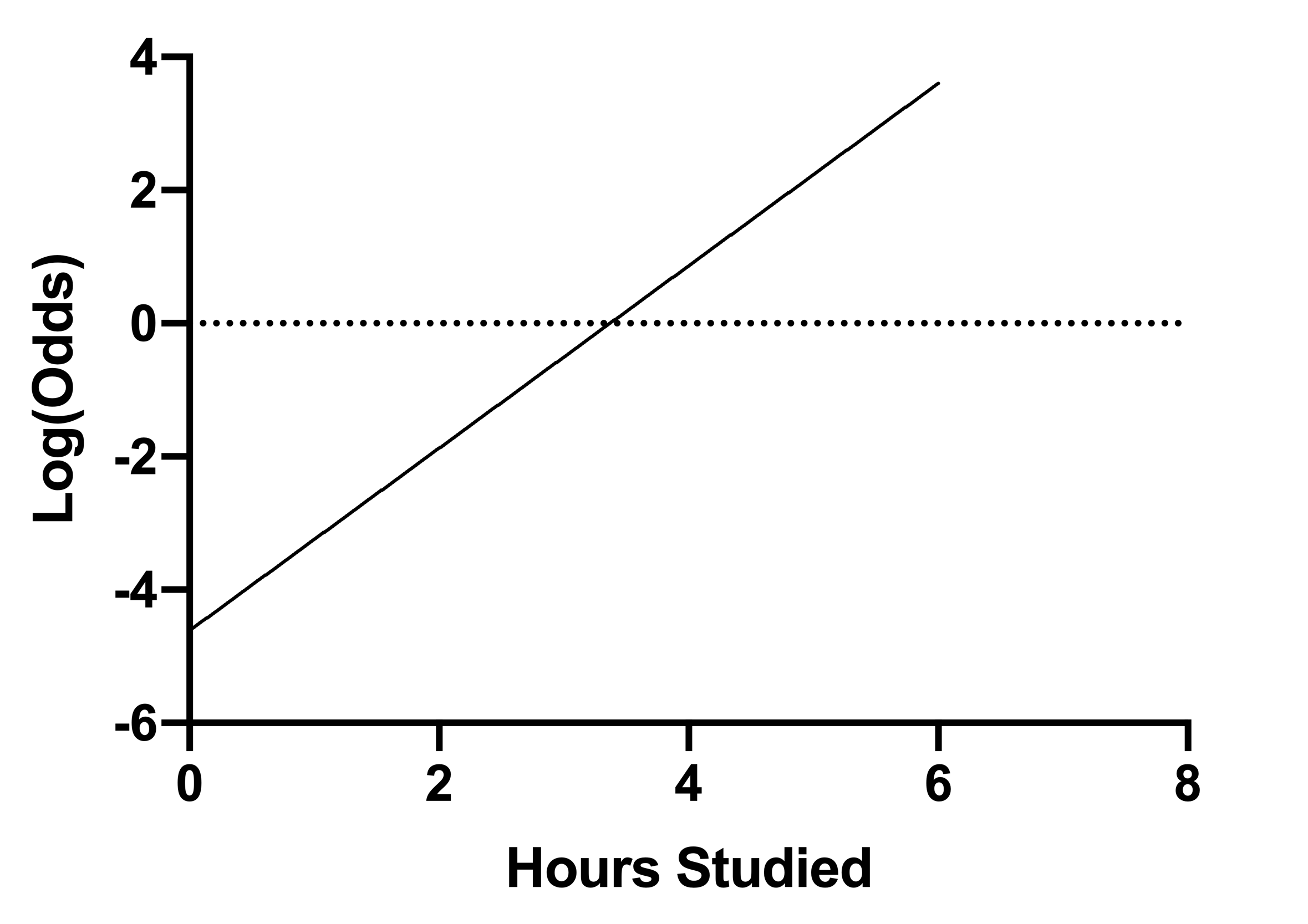
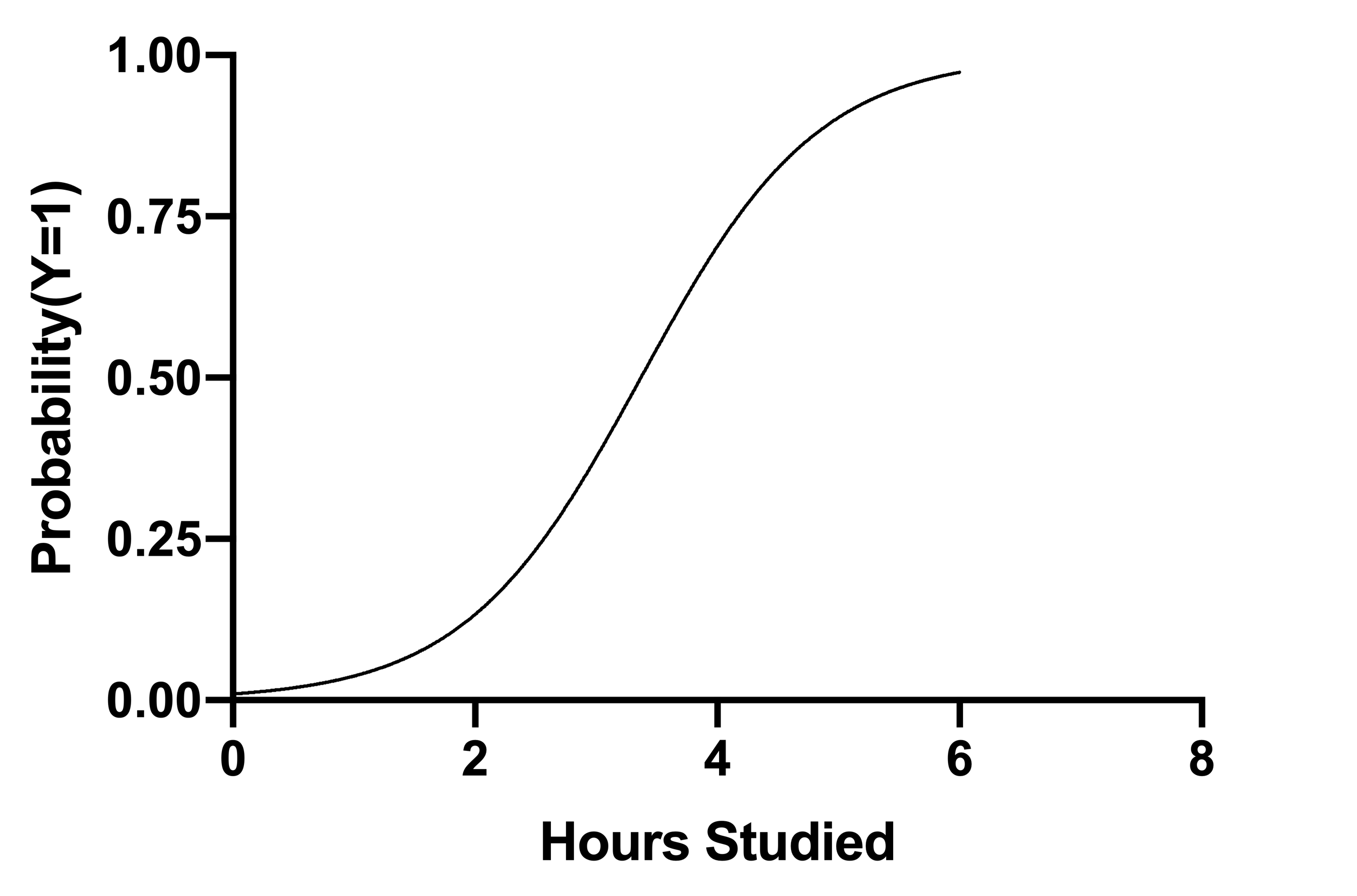
Often, β0 and β1 will be referred to as the "intercept" and "slope" of the simple logistic regression, respectively. Note that these terms only relate to the graph of the regression when Log(Odds) is plotted on the Y axis (see below). Typically, however, probability of Y=1 is plotted on the Y axis, generating the characteristic S-shaped logistic curve:
Probability Y=1 vs. X
β0 = -4.614, β1 = 1.370
Log Odds vs. X
β0 = -4.614, β1 = 1.370