Introduction
Sine waves describe many oscillating phenomena.
Step by step
Create an XY data table. There is one X column, and one or many Y columns. If you have several experimental conditions, place the first into column A, the second into column B, etc.
After entering data, click Analyze, choose nonlinear regression, choose the panel of equations for sine waves, and choose Standard sine wave.
If you know the Y value must equal zero at time zero, then constrain PhaseShift to a constant value of zero.
You may need to fuss with the initial values for PhaseShift and Wavelength, as our built-in rules for computing the initial value rarely work.
•For Wavelength. Count the number of peaks between two values X = a and X = b and set the initial value for Wavelength to 1/( NumberOfPeaks / (b - a)).
•For PhaseShift. If Y=0 at X=0, then PhaseShift is zero. If Y is at its maximum when X=0, then PhaseShift=3.14159. Interpolate in between if necessary.
Model
Y= Amplitude*sin((2*pi*X/Wavelength)+PhaseShift)
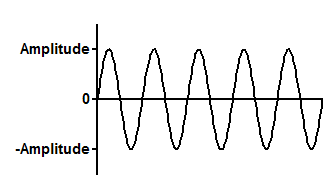
Interpret the parameters
Amplitude is the height of top of the waves, in Y units. If Prism reports a negative Amplitude but you expect a positive Amplitude, simply change the initial value of the PhaseShift by Pi in either direction.
Wavelength is the time it takes for a complete cycle, in units of X
Frequency is the number of cycles per time unit. It is calculated as the reciprocal of wavelength, and is expressed in the inverse of the time units of X.
PhaseShift in radians. A PhaseShift of 0 sets Y equal to 0 at X=0. A PhaseShift of pi sets Y equal to its maximum when X=0. If the best-fit value of PhaseShift surprises you, remember that the sine wave oscillates. You can add or subtract 2*pi from phaseshift to get a different but equivalent phaseshift. Fussing with the initial values can get Prism to fit the one you want.