Prism can interpolate values from linear or nonlinear standard curves (calibration curve). When the standard curve is nonlinear, people sometimes ask whether Prism can determine a section in the middle of the curve that is linear -- the "linear range".
Prism does not help you determine a "linear range" for several reasons.
•There is no need to restrict analysis to a linear range. If you fit a curve with nonlinear regression, you can interpolate from all parts of the curve. It doesn't make sense to define a somewhat arbitrary linear range, and then analyze just those values with linear regression.
•You can't use a "linear range" as a way to make sure that the interpolated value is precise. Even with linear regression, interpolating in the middle of the concentrations of the standards is more precise than interpolating near the highest or lowest concentrations. With both linear and nonlinear regression, Prism can report a confidence interval of the interpolated values.
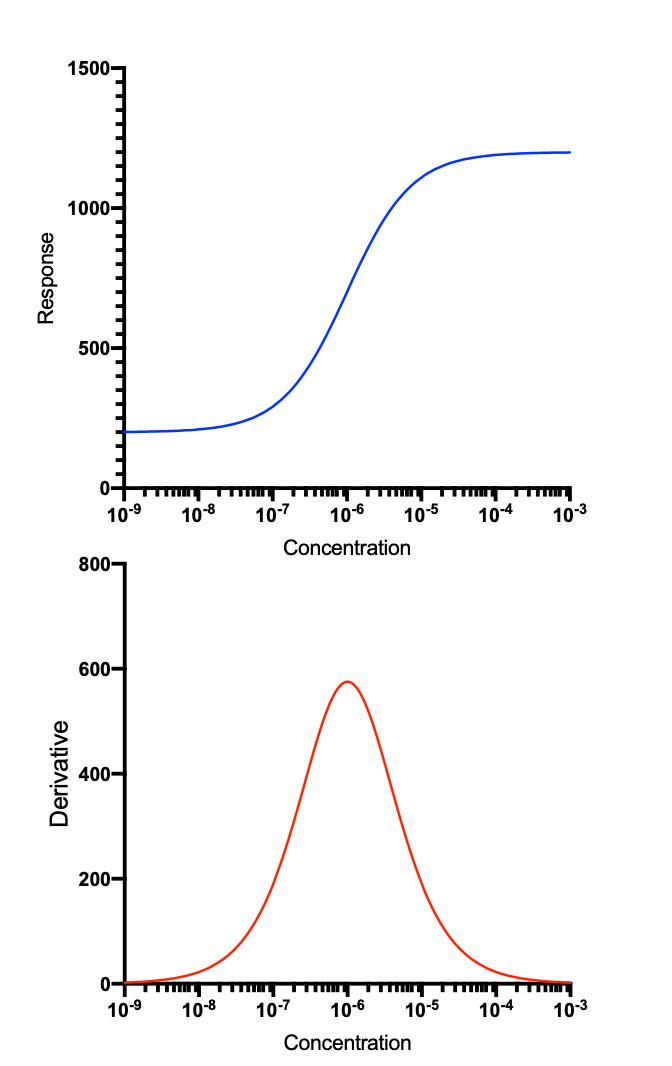
•There is no clear definition of a "linear range". Any such definition is arbitrary. The graph below shows an ideal log(concentration) vs. response curve. It looks like there is a "linear range" in the middle of the curve. But the lower graph shows the derivative (slope) of the curve. If there were a linear part of the curve, the derivative curve would be flat (horizontal) where the slope of the curve doesn't change (because it is "linear"). Because there is no flat portion of the derivative curve, any definition of "linear portion" would be arbitrary.