Repeated measures defined

Repeated measures means that the data are matched. Here are some examples:

•You measure a dependent variable in each subject several times, perhaps before, during and after an intervention.

•You recruit subjects as matched groups, matched for variables such as age, ethnic group, and disease severity.

•You run a laboratory experiment several times, each time with several treatments handled in parallel. Since you anticipate experiment-to-experiment variability, you want to analyze the data in such a way that each experiment is treated as a matched set.  Although you don’t intend it, responses could be more similar to each other within an experiment than across experiments due to external factors like more humidity one day than another, or unintentional practice effects for the experimenter.

Matching should not be based on the variable you are comparing. If you are comparing blood pressures in three groups, it is OK to match based on age or zip code, but it is not OK to match based on blood pressure.

The term repeated measures applies strictly only when you give treatments repeatedly to one subject (the first example above). The other two examples are called randomized block experiments (each set of subjects is called a block, and you randomly assign treatments within each block). The analyses are identical for repeated measures and randomized block experiments, and Prism always uses the term repeated measures.

Matching by which factor(s)?

If your data are matched, choose which of the two factors are repeated measures, or if both factors are repeated measures. If one factor is repeated measures and the other is not, this analysis is also called mixed effects model ANOVA.

Choose carefully, as the results can be  very misleading if you make a choice that doesn't correspond to the experimental design. The choices are:

No matching. Use regular two-way ANOVA (not repeated measures).

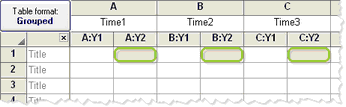
Each column represents a different repeat, so matched values are spread across a row.

Each row represents a different time point, so matched values are stacked into a subcolumn.

Repeated measures by both factors.

Take your time when making this choice.We find that too many people think "repeated measures" but don't take the time to carefully specify which factor is repeated or if both factors are repeated. If your choice here doesn't match your actual experimental design, the results will probably be incorrect.

Assume sphericity?

With two-way repeated measures ANOVA, choose whether to assume sphericity. If you do not assume sphericity, Prism uses the the Greenhouse-Geisser correction and calculates epsilon.

The assumption of sphericity states that the variance of the differences between treatment A and B equals the variance of the difference between A and C, which equals the variance of the differences between A and D, which equals the variance of the differences between B and D...  (Or, when repeated measures are stacked in subcolumns, that the variance of the differences between treatment 1 and 2 equals the variance of the difference between 1 and 3...) Like all statistical assumptions, this assumption pertains to the populations from which the data were sampled, and not just to these particular data sets.

Note that if the factor with repeated measures has only two levels, then there is no reason to be concerned about violations of sphericity. For example if each subject is measured before and after a treatment, and there are four different treatments, there would be no need to worry about sphericity, since the repeated measures factor only has two levels (before and after). If you ask for the Greenhouse-Geisser correction with only two levels of the repeated measures factor, the results will be identical to what they would have been if you hadn't chosen that option and the reported value of epsilon will be 1.0000000.