How Prism computes the geometric mean
Compute the logarithm of all values, compute the mean of the logarithms, and then take the antilog. Prism uses base 10 (common) logarithms, and then takes ten to the power of the mean of the logarithms to get the geometric mean. This is equivalent to multiplying all the values together and taking that product to the 1/n power, where n is the number of values.
Geometric means are often used to average ratios.
It makes sense to use the geometric mean when the set of logarithms of the data form a symmetrical approximately Gaussian distribution.
How Prism computes the geometric SD
First, transform all the values to logarithms, compute the sample SD of those log values, and then take the antilogarithm of that SD. Prism uses base 10 (common) logarithms, and then takes ten to the power of the mean of the logarithms to get the geometric mean.
The geometric SD factor has no units. It is a unitless ratio.
It makes no sense to add the geometric SD to the geometric mean (or any other value), and makes equally no sense to ever subtract the geometric SD from the geometric mean. The geometric SD is a value you always multiply or divide by. The range from (the geometric mean divided by the geometric SD factor) to (the geometric mean multiplied by the geometric SD factor) will contain about two thirds of the values if the data are sampled from a lognormal distribution. Similarly, the range from (the mean minus the SD) to (the mean plus the SD) will contain about two thirds of the values when data are sampled from a Gaussian distribution.
How to report the geometric mean and SD
While it is common to see a data sampled from a Gaussian distribution reported as, "The mean is 3.2 ± 1.2 (SD)", it is currently rare to report data sampled from a lognormal distribution reported as, "The geometric mean is 4.3 *÷ 1.14." But that kind of reporting makes sense. Instead of using a symbol meaning "plus or minus" which makes sense for data sampled from a Gaussian distribution, use symbols meaning "times or divided by" when reporting results from data sampled from a lognormal distribution.
Example
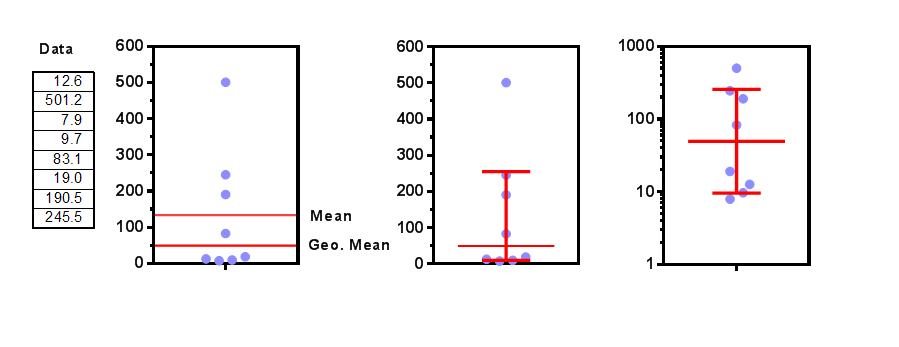
The example above shows eight values (so you can do the calculations yourself, if you want to). The geometric mean is 49.55 and the geometric SD factor is 5.15. The left graph shows the data with lines denoting the mean and geometric mean. The middle graph shows how Prism plots the geometric mean and geometric SD. The upper error bar extends up to the geometric mean times the geometric SD factor (49.55 * 5.15 = 255.2). The lower error bars extends down to the geometric mean divided by the geometric SD factor (49.55 / 5.15 = 9.62). The right graph shows the data, the geometric mean, and the geometric SD plotted on a logarithmic axis. The log SD error bars appear visually symmetrical on a log axis, even though numerically they are very asymmetrical.