|
Navigation: STATISTICS WITH PRISM 8 > Survival analysis > Intepreting results: Survival analysis Q&A: Survival analysis |
Scroll Prev Top Next More |
Prism offers two choices. •The symmetrical method was the only method offered in Prism 4 and earlier, and is offered now for compatibility. It uses the method of Greenwood. We don't recommend it. •The asymmetrical method is more accurate and recommended. It is explained on page 42 and page 43 of Machin. That book does not give a name or reference for the method, The idea is that it first does a transform (square root and log) that makes the uncertainty of survival close to Gaussian. It then computes the SE and a symmetrical 95% CI on that transformed scale. Then it back transforms the confidence limits back to the original scale. |
Survival analysis computes the median survival with its confidence interval. The reason for this is that the median survival time is completely defined once the survival curve descends to 50%, even if many other subjects are still alive. And the median survival is defined, even if data from some subjects was censored. In contrast, the mean survival is simply not defined until every subject dies, and only when you know the survival time for each subject (none were censored). These conditions occur in very very few studies, so Prism doesn't compute mean survival. But there is an easy workaround: If you know he survival times for each subject, enter them into a column table, and ask Prism to do column statistics to calculate the mean with its confidence interval. |
 Can Prism create a survival curve when you already know the percent survival at each time?
Can Prism create a survival curve when you already know the percent survival at each time?
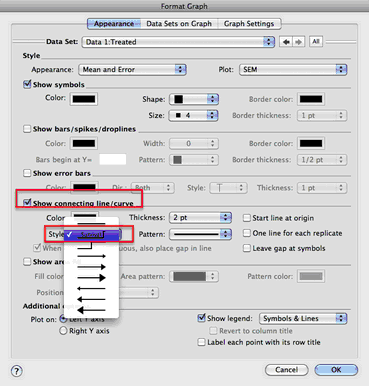
Prism can create Kaplan-Meier survival curves, and compare these with the logrank test (or the Wlcoxon-Gehan-Breslow test). To do this, you must enter data on a Prism table formatted as a survival table and you must enter one row of data per subject. But what if you already know the percent survival at each time point, and just want to make a graph? In this case, do not enter data onto a survival data table. That table requires information about each subject. Instead, create an XY data table. If you only want to enter percent survival, format the data table to enter single Y values with no subcolumns. If you know the standard error of the survival at each time point (from calculations done elsewhere), then format the data table for entry of mean with SEM (in fact, the "mean" will be percent survival, and "SEM" will be SE of the survival percentage). Enter time (as months or days or weeks) into X. You must enter this as a number, not a date. Enter percent (or fraction) survival into Y. Just enter the values (don't append percent symbols). Then polish your graph. If you want the graph to have a staircase look (which is traditional for survival curves), you can do that. This screen shot shows where to make this setting in the Format Graph dialog:
If you enter survival percentages on an XY table, it will not be possible to do any calculations. You won't be able to compute error bars or confidence bands, and wont' be able to compare survival curves under different treatments. |
If there are no censored observationsIf you follow each subject until the event occurs (the event is usually death, but survival curves can track time until any one-time event), then the curve will eventually reach 0. At the time (X value) when the last subject dies, the percent survival is zero. If all subjects are followed for exactly the same amount of timeIf all subjects are followed for the same amount of time, the situation is easy. If one third of the subjects are still alive at the end of the study, then the percent survival on the survival curve will be 33.3%. If some subjects are censored along the wayIf the data for any subjects are censored, the bottom point on the survival curve will not equal the fraction of subjects that survived. Prior to censoring, a subject contributes to the fractional survival value. Afterward, she or he doesn't affect the calculations. At any given time, the fractional (or percent) survival value is the proportion of subjects followed that long who have survived. Subjects whose data are censored --either because they left the study, or because the study ended--can't contribute any information beyond the time of censoring. So if any subjects are censored before the last time shown on the survival curve's X-axis, the final survival percentage shown on the survial graph will not correspond to the actual fraction of the subjects who survived. That simple survival percentage that you can easily compute by hand is not meaningful, because not all the subjects were not followed for the same amount of time. When will the survival curve drop to zero?If the survival curve goes all the way down to 0% survival, that does not mean that every subject in the study died. Some may have censored data at earlier time points (either because they left the study, or because the study ended while they were alive). The curve will drop to zero when a death happens after the last censoring. Make sure your data table is sorted by X value (which Prism can do using Edit..Sort). Look at the subject in the last row. If the Y value is 1 (death), the curve will descend to 0% survival. If the Y value is 0 (censored), the curve will end above 0%. |
Median survival is the time it takes to reach 50% survival. If more than 50% of the subjects are alive at the end of the study, then the median survival time is simply not defined. The P value comes from the logrank test, which compares the entire curve, and works fine even if the percent survival is always greater than 50%. Two curves can be very different, even if they never dip down below 50%. |
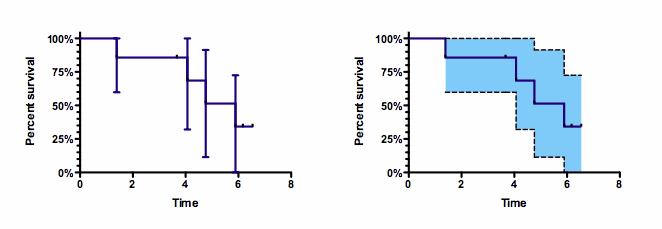
When Prism computes survival curves, it can also compute the 95% confidence interval at each time point (using two alternative methods). The methods are approximations, but can be interpreted like any confidence interval. You know the observed survival percentage at a certain time in your study, and can be 95% confident (given a set of assumptions) that the confidence interval contains the true population value (which you could only know for sure if you had an infinite amount of data). When these confidence intervals are plotted as error bars (left graph below) there is no problem. Prism can also connect the ends of the error bars, and create a shaded region (right graph below). This survival curve plots the survival of a sample of only seven people, so the confidence intervals are very wide. Prism file. The shaded region looks like the confidence bands computed by linear and nonlinear regression, so it is tempting to interpret these regions as confidence bands. But it is not correct to say that you can be 95% certain that these bands contain the entire survival curve. It is only correct to say that at any time point, there is a 95% chance that the interval contains the true percentage survival. The true survival curve (which you can't know) may be within the confidence intervals at some time points and outside the confidence intervals at other time points.
It is possible (but not with Prism) to compute true confidence bands for survival curves, and these are wider than the confidence intervals shown above. Confidence bands that are 95% certain to contain the entire survival curve at all time points are wider than the confidence intervals for individual time points. |
When analyzing survival data, Prism simply ignores any rows with X=0. Our thinking is simple. If alternative treatments begin at time zero, then a death right at the moment treatment begins provides no information to help you decide which of two treatments is better. There is no requirement that X be an integer. If a death occurs half a day into treatment, and X values are tabulated in days, enter 0.5 for that subject. Some fields (pediatric leukemia is one) do consider events at time zero to be valid. These studies to not simply track death, but track time until recurrence of the disease. But disease cannot recur until it first goes into remission. In the case of some pediatric leukemia trials, the treatment begins 30 days before time zero. Most of the patients are in remission at time zero. Then the patients are followed until death or recurrence of the disease. But what about the subjects who never go into remission? Some investigators consider these to be events at time zero. Some programs, we are told, take into account the events at time zero, so the Kaplan-Meier survival curve starts with survival (at time zero) of less than 100%. If 10% of the patients in one treatment group never went into remission, the survival curve would begin at Y=90% rather than 100%. We have not changed Prism to account for deaths at time zero for these reasons: •We have seen no scientific papers, and no text books, that explains what it means to analyze deaths at time zero. It seems far from standard. •It seems wrong to combine the answers to two very different questions in one survival curve: What fraction of patients go into remission? How long do those in remission stay in remission? •If we included data with X=0, we are not sure that the results of the survival analysis (median survival times, hazard ratios, P values, etc.) would be meaningful. The fundamental problem is this: Survival analysis analyses data expressed as the time it takes until an event occurs. Often this event is death. Often it is some other well defined event that can only happen once. But usually the event is defined to be something that could possibly happen to every participant in the trial. With these pediatric leukemia trials, the event is defined to be recurrence of the disease. But, of course, the disease cannot recur unless it first went into remission. So the survival analysis is really being used to track time until the second of two distinct events. That leads to the problem of how to analyze the data from patients who never go into remission (the first event never happens). We are willing to reconsider our decision to ignore, rather than analyze, survival data entered with X=0. If you think we made the wrong decision, please let us know. Provide references if possible. There is a simple work around if you really want to analyze your data so deaths at time zero bring down the starting point below 100%, enter some tiny value other than zero. Enter these X values, say, as 0.000001. An alternative is to enter the data with X=0, and then use Prism's transform analysis with this user-defined transform: X=IF(X=0, 0.000001, X) In the results of this analysis, all the X=0 values will now be X=0.000001. From that results table, click Analyze and choose Survival analysis. |
Prism uses the Kaplan-Meier method to compute percentage survival. This is a standard method. The only trick is in accounting for censored observations. Consider a simple example. You start with 16 individuals. Two were censored before the first death at 15 months. So the survival curve drops at 15 months from 100% down to 13/14=92.86%. Note that the denominator is 14, not 16. Just before the death, only 14 people were being followed, not 16 (since data for two were censored before that). Seven more individuals were censored before the next death at 93 months. So of those who survived more than 15 months, 5/6= 83.3% were alive after 93 months. But this is a relative drop. To know the percent of people alive at 0 months who are still alive after 93 months, multiply 92.86% (previous paragraph) times 83.33% and you get 77.38%, which is the percent survival Prism reports at 93 months. Now you can see why these Kaplan-Meier calculations are sometimes called the product-limit method. |
Reference
David Machin, Yin Bun Cheung, Mahesh Parmar, Survival Analysis: A Practical Approach, 2nd edition, IBSN:0470870400.
© 1995-2019 GraphPad Software, LLC. All rights reserved.