|
More accurate (asymmetrcial) confidence intervals from nonlinear regression |
Scroll Prev Top Next More |
With all prior versions of Prism, the confidence intervals for parameters fit by nonlinear regression were always symmetrical around the best-fit value. These are called asymptotic intervals or approximate intervals. These are are what most nonlinear regression programs report. But the true uncertainty in a parameter's value, in many cases, is asymmetrical. In these cases, the symmetrical confidence intervals do not really express the precision of a parameter's estimate very well.
Prism 7 lets you choose to create asymmetrical confidence intervals instead. Based on the method used to compute these intervals, they are sometimes called profile likelihood intervals. These almost always do a better job of expressing the precision of the parameter estimate, and in some cases a much better job.
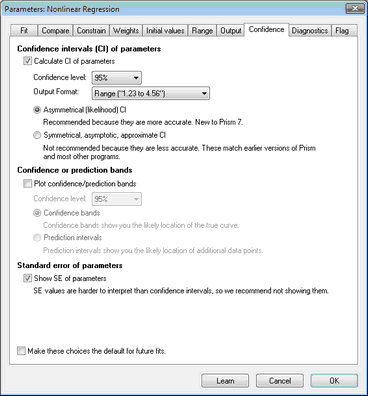
The initial default is to show the asymmetrical intervals, but you can change this default (in the Confidence tab of the nonlinear regression dialog). Since the only purpose of the standard errors of the parameters is to compute the approximate confidence intervals, we suggest that you stop showing these once you get used to the new asymmetrical intervals.
The only disadvantage of this new way of computing the confidence interval is that the calculations are slower. But with modest data sets (few dozen data points), standard models, and reasonably fast computers, you won't notice. Prism 7 computes nonlinear regression more quickly than prior versions (about ten times faster if you choose a built-in equation), so you are unlikely to notice the slow down.
The availability of these new asymmetrical confidence intervals let us add new dose-response equations where X is dose or concentration, rather than the logarithm of dose or concentration.