The next tab is titled “Loadings”, and provides information related to a topic discussed previously in this guide, but not mentioned explicitly. This table includes the loadings for each selected PC as a separate column, and lists each original variable on a separate row. While a single loading is defined by a set of multiple values (one value for each individual variable), these individual values are the correlation between the specific variable and the PC that the loading is calculated for.

In other words, the loadings for any given PC provide information on how correlated each variable is with that PC. Taken as a whole, this is another way of looking at how “aligned” the PC is with each of the original variables. This is very similar to the concept of eigenvectors for PCs. Remember that eigenvectors represent the coefficients for the linear combination of variables that define PCs. A single eigenvector is defined by multiple values, with one coefficient value for each of the original variables. These coefficients also provide information on how well aligned the PC is with each of the variables: larger coefficients indicate more influence of that variable on the PC.

Recall also that eigenvectors for PCs always have a length of 1. This is where the relationship of loadings, eigenvectors, and eigenvalues all comes together:

Eigenvectors are unit-scaled loadings!

There’s a bit of fancy math that can be done to prove this relationship, but the bottom line is that eigenvectors have a length of 1, and loadings are just “scaled” versions of the eigenvectors. Scaled by what? The eigenvalues! Technically the square root of the eigenvalues. Here’s the full relationship:

Loading = Eigenvector * √(Eigenvalue)

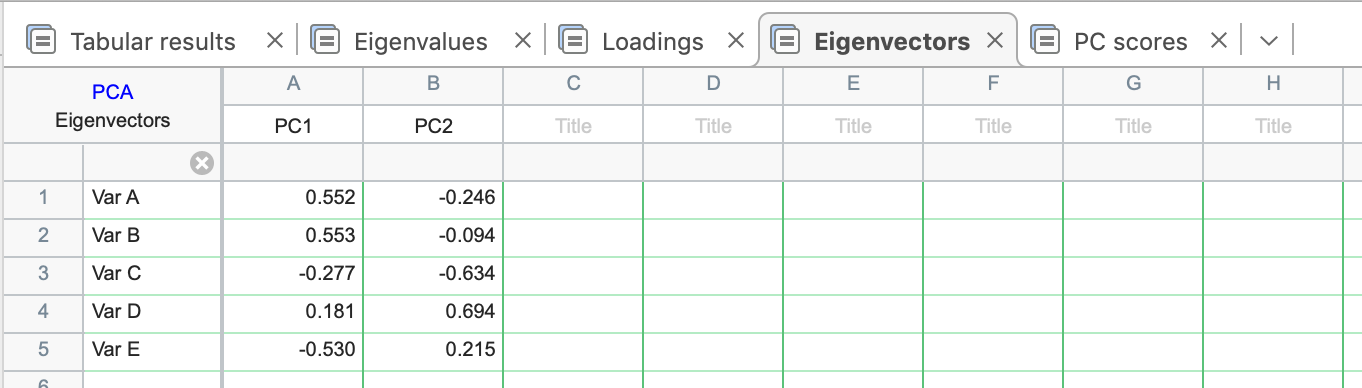
Loadings can also be used to visualize the relative strengths of correlations between variables using a Loadings plot (discussed later). Below are the loadings table and eigenvectors table (not shown by default) for PCA of our example data.

Loadings

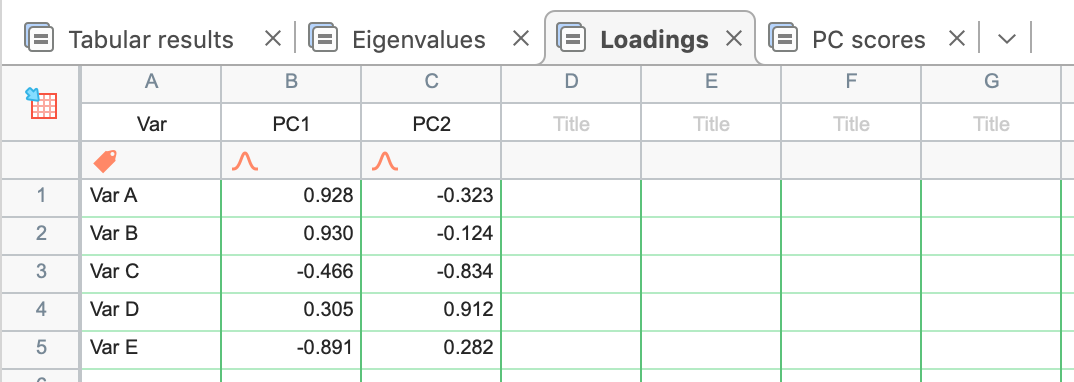
Eigenvectors