Introduction
If the enzyme has cooperative subunits, the graph of enzyme velocity as a function of substrate concentration will appear sigmoidal. Prism offers one empirical equation for fitting sigmoidal substrate-velocity curves. Read advanced books on enzyme kinetics for alternative methods based on molecular models of allosteric action.
How to enter data
Create an XY data table. Enter substrate concentration into X, and enzyme velocity into Y. If you have several experimental conditions, place the first into column A, the second into column B, etc.
After entering data, click Analyze, choose nonlinear regression, choose the panel of enzyme kinetics equations, and choose Allosteric sigmoidal enzyme kinetics.
The model
Y=Vmax*X^h/(Khalf^h + X^h)
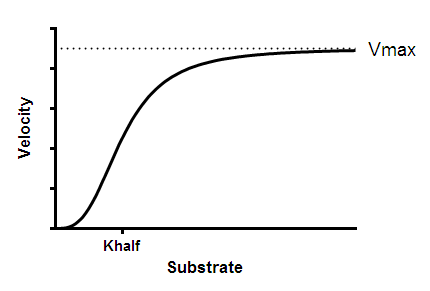
Interpret the parameters
Vmax is the maximum enzyme velocity in the same units as Y. It is the velocity of the enzyme extrapolated to very high concentrations of substrate, and therefore is almost always higher than any velocity measured in your experiment.
Khalf is the concentration of substrate that produces a half-maximal enzyme velocity. It is the EC50.
h is the Hill slope. When h=1, this equation is identical to the standard Michaelis-Menten equation. When it is greater than 1.0, the curve is sigmoidal due to positive cooperativity. The variable h does not always equal the number of interacting binding sites, but its value can not exceed the number of interacting sites. Think of h as an empirical measure of the steepness of the curve and the presence of cooperativity.
Kprime is related to the Km. It is computed as Khalf^h, and is expressed in the same units as X.
An alternative form of the equation
An alternative version of the equation (equation 5.47 in the book by Dr. Copeland referenced below) fits Kprime.
Y=Vmax*X^h/(Kprime + X^h)
Note that Kprime in this equation equals Khalf^h in the equation built in to Prism. The two models generate exactly the same curve, and simply have alternative methods for reporting the parameters. Prism reports both Kprime and Khalf.