Introduction
Kcat is the turnover number -- the number of substrate molecule each enzyme site converts to product per unit time. If you know the concentration of enzyme sites, you can fit Kcat instead of Vmax when analyzing a substrate vs. velocity curve.
The model
Y = Et*kcat*X/(Km + X)
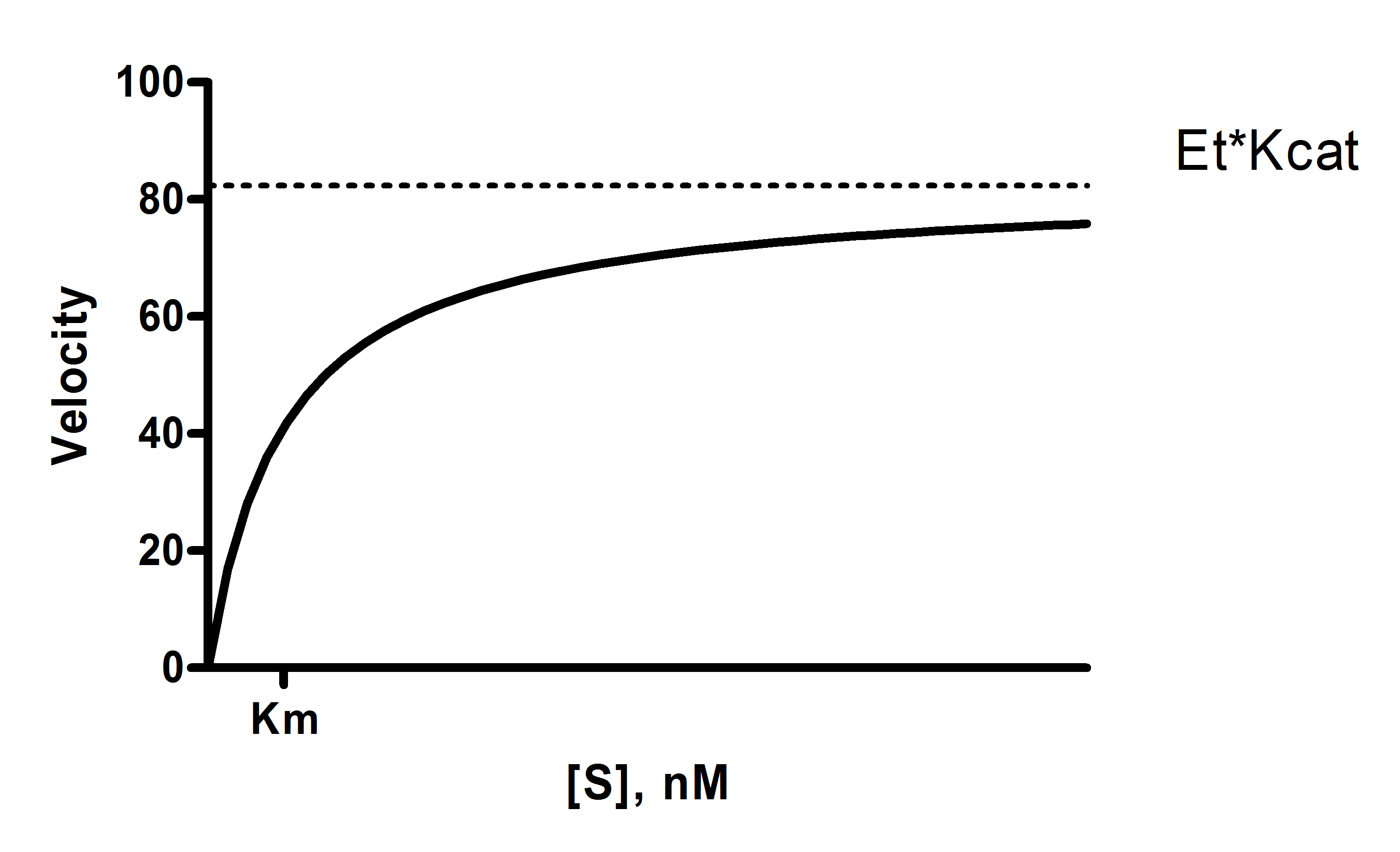
X is the substrate concentration.
Y is enzyme velocity.
kcat is the turnover number, the number of times each enzyme site converts substrate to product per unit time. This is expressed in the inverse of the time units of the Y axis. For example, if Y is in micromoles of substrate per minute, then kcat is the number of molecules of substrate produced per catalytic site per minute.
Km is the Michaelis-Menten constant, in the same units as X. It is the substrate concentration needed to achieve a half-maximum enzyme velocity.
Et is the concentration of enzyme catalytic sites. If the enzyme has multiple subunits, note that Et is the concentration of catalytic sites, which can be larger than the concentration of enzyme molecules. The Y values you enter are enzyme velocity entered in units of concentration per time. Et must be entered in those same concentration units (while the time units are defined by kcat).
Vmax is the maximum enzyme velocity in the same units as Y. It is not directly shown in the model above. It is the velocity of the enzyme extrapolated to very high concentrations of substrate, so is almost always higher than any velocity measured in your experiment. It is computed by multiplying Et times kcat.
Relationship to the Michaelis-Menten model
The curve shown above is identical to the curve defined by the Michaelis-Menten model. You'll get identical curves when you fit either model to your data, and identical values for Km.
The Michaelis-Menten model finds the Vmax, which is the maximum enzyme velocity extrapolated out to very high concentrations of substrate. It is expressed in the same units you used to enter your Y values (enzyme activity). Usually it is straightforward to express this (or convert to ) moles/minute/mg of protein. The Vmax is determined by how many enzyme sites are present (Et) and the rate at which the enzyme can convert substrate to product (kcat).
If you know the concentration of enzyme sites you've added to the assay (Et) then you can fit the catalytic constant Kcat using the model above.
When calculating Kcat, the concentration units cancel out, so Kcat is expressed in units of inverse time. It is the turnover number -- the number of substrate molecule each enzyme site converts to product per unit time.
Fitting the model with Prism
1.Create an XY data table. Enter substrate concentration into X, and enzyme velocity into Y. If you have several experimental conditions, place the first into column A, the second into column B, etc. You can also choose Prism's sample data: Enzyme kinetics -- Michaelis-Menten.
2.After entering data, click Analyze, choose nonlinear regression, choose the panel of enzyme kinetics equations, and choose Kcat.
3.You must constrain Et to a constant value, based on other experiments. To constrain the value of Et, go to the Constrain tab of the nonlinear regression dialog, make sure that the drop down next to Et is set to "Constant equal to" and enter the value. For the sample data, enter 100 as the value of Et.
If you don't know the value of Et, you cannot fit the kcat, but instead should fit the Vmax. It is not possible for Prism to fit both the kcat and Et, as the two parameters are intertwined, and a substrate-velocity curve gives no information about their individual values.
4.With the sample data, Prism reports that Km= 5.886 with a 95% confidence interval ranging from 3.933 to 7.839. The best fit value of kcat is 13.53 with a 95% confidence interval ranging from 11.97 to 15.09.
Notes
•See the list of assumptions of all analyses of enzyme kinetics.
•This equation fits exactly the same curve as the equation that fits Vmax, rather than the turnover number Kcat.
•