What are confidence and prediction bands?
The 95% confidence bands enclose the area that you can be 95% sure contains the true curve. It gives you a visual sense of how well your data define the best-fit curve. It is closely related to the 95% prediction bands , which enclose the area that you expect to enclose 95% of future data points. This includes both the uncertainty in the true position of the curve (enclosed by the confidence bands), and also accounts for scatter of data around the curve. Therefore, prediction bands are always wider than confidence bands. How confidence and prediction bands are computed.

How to plot confidence bands, prediction bands or both
Choose to plot confidence or prediction bands by an checking option on the Confidence tab.
Prism lets you choose either a confidence band or a prediction band, but not both. To plot both on one graph, you need to analyze your data twice, choosing a confidence band the first time and a prediction band the second time.
The regression lines or curves are data sets that you can add to any graph by drag-n-drop or using the Change menu from the graph.
Prism can also show you the XY coordinates that define the curve and confidence bands (or prediction bands). To see this table, click the icon to the right of the results tabs to show a list of all results tabs. View the one labeled 'Curve'. For each X value, you'll see the Y value and the distance the confidence or prediction curve is above and below that value.
How to plot a one-sided confidence or prediction band
In some situations, it makes sense to plot only one side of the confidence or prediction band. One use for a one-sided confidence band would be on a graph that plots purity of a substance over time. You want to know, with a certain confidence, how low the purity could be at a certain time. But you don't really care about quantifying how high the purity could be.
To plot a one sided 95% confidence or prediction band:
1.Check the option (on the Diagnostics tab) to plot "90%" confidence (or prediction) bands. When you plot in only one direction, this is really a 95% confidence band.
2. On the Format Graph dialog, choose the data set that defines regression curve and make sure that error bars are turned on with the "---" style.
3.Choose to plot those error bands in one direction.

Do not mix up confidence intervals and confidence bands
It is easy to mix up confidence intervals and confidence bands. Choose both on the Confidence tab.
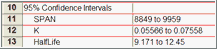
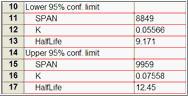
The 95% confidence interval tells you how precisely Prism has found the best-fit value of a particular parameter. It is a range of values, centered on the best-fit value. Prism can display this range in two formats:
|
|
Don't mix up confidence bands and prediction bands
Note the difference between confidence and prediction bands:
The 95% confidence bands enclose the area that you can be 95% sure contains the true curve. If you have many data points, the confidence bands will be near the line or curve, and most of your data will lie outside the confidence bands.
The 95% prediction bands enclose the area that you expect to enclose 95% of future data points. They are wider than confidence bands -- much wider with large data sets.
Situations where Prism won't plot confidence or prediction bands
Prism will not plot confidence or prediction bands in several situations:
•If the best-fit value of a parameter hits a constraint, the fit is unlikely to be useful. Prism does not plot confidence or prediction bands, because they would almost certainly be misleading.
•If the results of nonlinear regression are ambiguous, the confidence or prediction bands would be super wide, maybe infinitely wide. They would not be useful, so Prism does not plot them.
•If you choose robust nonlinear regression, Prism does not compute confidence or prediction bands, as it cannot compute standard errors or confidence intervals of the parameters.
•The fit is perfect. If the sum-of-squares is 0.0 and R2 is 1.0, it is not possible to compute or interpret confidence or prediction bands.
•If the fit is interrupted, confidence and prediction bands are not computed.
•If you chose to weight by 1/SD2. To compute confidence or prediction bands, Prism needs to be able to compute the weights for any value of X. When you weight by 1/SD2, weights are only known at the X values of the data, but not for other X values, so Prism cannot compute prediction or confidence bands.