Introduction
You cannot determine the association rate constant by simply observing the association of a single concentration of radioligand. The rate at which a ligand reaches equilibrium is determined not only by the association rate constant and the ligand concentration, but also by the dissociation constant.
One way to determine the association rate constant is to globally fit data obtained with two different concentrations of radioligand. An alternative approach, explained here is to measure association and dissociation in one experiment.
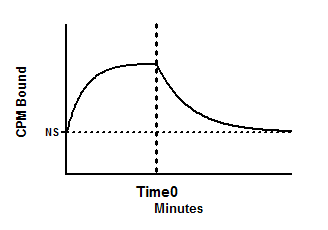
Add a radioligand and measure total binding at multiple time points, then at Time0 initiate dissociation (by adding an antagonist or by massive dilution) and then measure dissociation at various times.
Step by step
Create an XY data table. Enter time in minutes into X, and total binding into Y.
From the table of specific binding, click Analyze, choose nonlinear regression, choose the panel of Kinetics Binding equations, and choose Association then dissociation.
Constrain HotNM ([radioigand in nM] and Time0 (time at which dissociation was initiated) to constant values. If you entered specific binding into the Y column, also constrain NS to a constant value of zero.
Model
Radioligand=HotNM*1e-9
Kob=[Radioligand]*Kon+Koff
Kd=Koff/Kon
Eq=Bmax*radioligand/(radioligand + Kd)
Association=Eq*(1-exp(-1*Kob*X))
YatTime0 = Eq*(1-exp(-1*Kob*Time0))
Dissociation= YatTime0*exp(-1*Koff*(X-Time0))
Y=IF(X<Time0, Association, Dissociation) + NS
Interpret the parameters
Koff is the dissociation constant in min-1.
Kon is the association constant in inverse minutes multiplied by inverse concentration.
KD is computed from Koff/Kon. Expressed in Molar units.
Bmax is the maximum binding at equilibrium with maximum concentration of radioligand, in units of Y axis. Unless you used a very high concentration of radioligand, Bmax will have a wide confidence interval as the experiment is not designed to determine Bmax.
NS is the nonspecific binding, in units of the Y axis. It is the Y value at time 0, and also the Y value at very late times after all the ligand has dissociated.