Introduction

An exponential decay equation models many chemical and biological processes. It is used whenever the rate at which something happens is proportional to the amount which is left. Here are three examples:

•When ligands dissociate from receptors, the number of molecules that dissociate in any short time interval is proportional to the number that were bound at the beginning of that interval. Equivalently, each individual molecule of ligand bound to a receptor has a certain probability of dissociating from the receptor in any small time interval. That probability does not get higher as the ligand stays on the receptor longer.

•When radioactive isotopes decay, the number of atoms that decay in any short interval is proportional to the number of undecayed atoms that were present at the beginning of the interval. This means that each individual atom has a certain probability of decaying in a small time interval, and that probability is constant. The probability that any particular atom will decay does not change over time. The total decay of the sample decreases with time because there are fewer and fewer undecayed atoms.

•When drugs are metabolized by the liver or excreted by the kidney, the rate of metabolism or excretion is often proportional to the concentration of drug in the blood plasma. Each drug molecule has a certain probability of being metabolized or secreted in a small time interval. As the drug concentration goes down, the rate of its metabolism or excretion goes down as well.

Entering data

Create an XY data table. Enter time into X, and response (binding, concentration ..) into Y. If you have several experimental conditions, place the first into column A, the second into column B, etc.

You can also choose a sample data set for exponential decay.

After entering data, click Analyze, choose nonlinear regression, choose the panel of exponential equations, and choose One phase decay.

Consider constraining Plateau to a constant value of zero

If you have subtracted off any background signal, then you know the curve has to plateau at Y=0. In this case, you should constrain the parameter Plateau to be a constant value equal to zero. To do this, go to the Constrain tab of the nonlinear regression dialog, set the drop down next to Plateau to "Constant equal to" and enter the value 0.0.

Model

Y=(Y0 - Plateau)*exp(-K*X) + Plateau

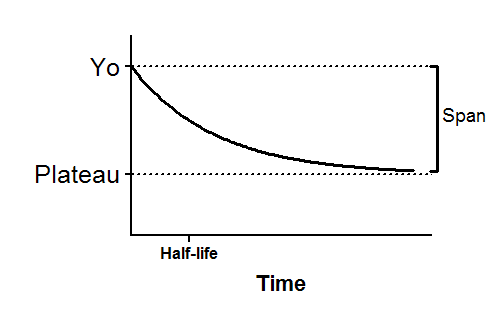
Y0 is the Y value when X (time) is zero. It is expressed in the same units as Y,

Plateau is the Y value at infinite times, expressed in the same units as Y.

K is the rate constant, expressed in reciprocal of the X axis time units. If X is in minutes, then K is expressed in inverse minutes.

Tau is the time constant, expressed in the same units as the X axis. It is computed as the reciprocal of K.

Half-life is in the time units of the X axis. It is computed as ln(2)/K.

Span is the difference between Y0 and Plateau, expressed in the same units as your Y values.

The derivative of an exponential decay  equals -K*Y. So the initial rate equals -K*Y0.