The usual steepness of a dose-response curve
Many dose-response curves follow the shape of a receptor binding curve. As shown below, 81 times more agonist is needed to achieve 90% response than a 10% response.

Since the linkage between agonist binding and response can be very complex, any shape is possible. It seems surprising, therefore, that so many dose-response curves have shapes almost identical to receptor binding curves, even when we know there are multiple steps between binding and measured response. It turns out that no matter how many steps intervene between agonist binding and response, the dose-response curve will have the usual steepness so long as each messenger binds to a single binding site according to the law of mass action.
The slope factor or Hill slope
Some dose-response curves are steeper or shallower than the standard curve. The steepness is quantified by the Hill slope, also called a slope factor. A dose-response curve with a standard slope has a Hill slope of 1.0. A steeper curve has a higher slope factor, and a shallower curve has a lower slope factor.
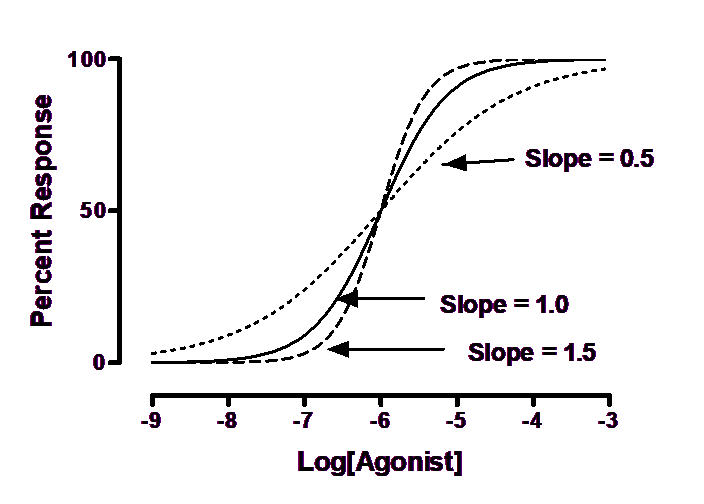
If you use a single concentration of agonist and varying concentrations of antagonist, the curve goes downhill and the slope factor is negative. The steeper the downhill slope, the more negative the Hill slope.
Standard slope or variable slope?
Because this standard slope is so common, Prism comes with equations with the standard slope built in. The equations that don't have 'variable slope' in their name assume the standard slope (1.0 for stimulation, -1.0 for inhibition).
Deciding whether to fit a model with a standard slope or a variable slope is not easy.
If you have lots of data points (more than a dozen, perhaps lots more), then you can fit the slope by picking a variable slope equation. If you have fewer data points, and a standard system, it makes sense to choose an equation with a standard slope.