A common use of nonlinear (and linear) regression is interpolating.The basic idea is simple:
1.Enter a standard curve, also called a calibration curve. Each point consists of a concentration (or logarithm of concentration) and a response. The responses are commonly radioactivity, fluorescence, or optical density. Standard curves are sometimes called calibration curves.
2.Fit a line or curve through the standards. For this purpose, you don't much care about the meaning of the model, or the interpretation of the best-fit values of the parameters (EC50, etc.).
3.For unknown samples, you know the response, but not the concentration. So read the concentration from the curve:
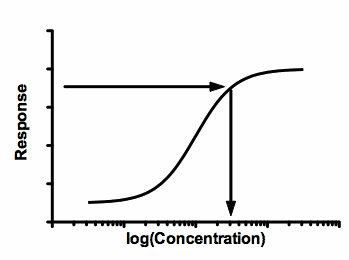
Notes:
•This graph shows the response going up as the concentration gets larger. In many cases, the response goes down as the concentration gets larger. Interpolation works in either case.
•Sigmoid shaped dose-response curves are commonly used with many assays. If the X values analyzed by the analysis are the logarithm of concentration, then so are the interpolated values. You need to take the antilogarithm of these values to return to concentration units.
•This example shows the most common use of interpolating. Finding an X value (concentration) for a given Y value. Prism can also interpolate the other way: Finding a Y value for an entered X value.