Choosing multiple comparisons for two-way ANOVA is not straightforward. Make this choice carefully, and after learning about two-way ANOVA. Consider getting help.
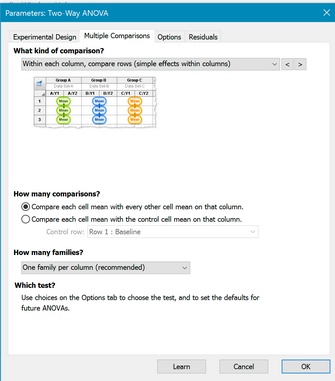
Which kind of comparison?
This is the most important decision. You need to pick a multiple comparison scheme that matches your scientific goal. The pictures, shown below and on the dialog, are probably more helpful than the explanations
The choices of comparisons (in the drop down) depend on the number of rows and columns in your data set.
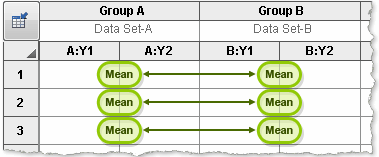
 Compare each cell mean with the other cell mean in that row
Compare each cell mean with the other cell mean in that row
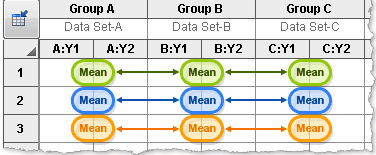
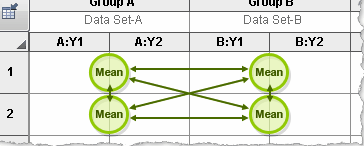
 Simple effects. Within each row, compare columns.
Simple effects. Within each row, compare columns.
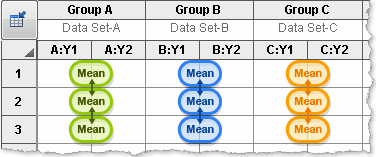
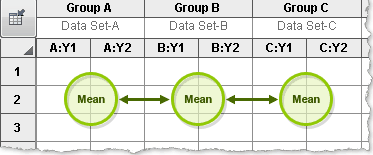
 Simple effects. Within each column, compare rows.
Simple effects. Within each column, compare rows.
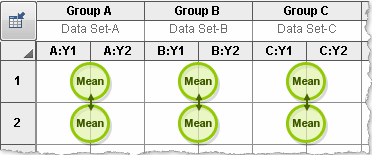
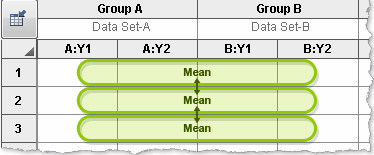
 Compare cell means regardless of rows and columns
Compare cell means regardless of rows and columns
How many comparisons?
Do you want to compare each mean (in the set) with each other mean? Or only compare each mean to the first, control, mean? The latter approach makes fewer comparisons, so has more power. The choice should be based on experimental design and the scientific questions you are asking.
How many families? (Applies to simple effects only.)
Multiple comparisons take into account the number of comparisons in the family of comparisons. The significance level (alpha) applies to the entire family of comparisons. Similarly, the confidence level (usually 95%) applies to the entire family of intervals, and the multiplicity adjusted P values adjust each P value based on the number of comparisons in a family.
If you choose to look at Simple effects (defined above), the definition of family is not obvious, and Prism offers two choices:
•One family for all comparisons. With this choice, there is always one family of comparisons for all rows (or all columns).This approach has less power, because it applies a stricter correction for multiple comparisons. This makes sense because there are more comparisons in the family.
•One family per column (or per row). Define the comparisons for each column (or each row) to be its own family of comparisons. With this choice, there are fewer comparisons per family (but more families), so comparisons have more power. We recommend this choice unless you have strong reason to consider all the comparisons to be one family.
The results page will repeat your choices, so it is clear how to interpret the results.
Prism 5.04 and 5.0d use the first definition of family (and do not offer you a choice of the other definition). If you wish to compare results with Prism 5, note this bug in releases of Prism 5 prior to 5.04 (Windows) and 5.0d (Mac).