ANOVA and repeated measures ANOVA
For most multiple comparisons tests, the first step is to compute the standard error of the difference between two mean using the equation below, where n1 and n2 are the sample sizes of the two means being compared and MSerror is the appropriate mean-square value from the ANOVA table.
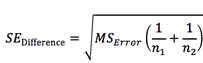
For one-way ANOVA or two-way ANOVA with no repeated measures, there is only one MSerror (or MSresidual) in the ANOVA table. For two-way ANOVA with repeated measures, see this document for the details of which MS value is used.
The equation above can be simplified a bit by first computing the pooled standard deviation:

Note that the MSerrror (and the pooled standard deviation) are computed from all the data in all the groups. The SE of the difference between means will the be same for all pairs of means if the samples sizes are equal.
Multiple comparisons after repeated measures ANOVA.
Multiple comparisons after fitting a mixed effects model
With repeated measures data, Prism lets you do repeated measures ANOVA or fit a mixed effects model. The two are equivalent when there are no missing values. When there are missing values, repeated measures ANOVA is impossible but it is still possible to fit a mixed effects model.
For multiple comparisons, the standard error of the difference is computed as sqrt(L*C*L'), where L is a vector/matrix of contrasts and C is a variance-covariance matrix at best-fit values.