Analyze repeated measures data with missing values.
Repeated measures ANOVA cannot be computed when even a single value is missing. This is a huge problem, and many people have asked us to do repeated measures ANOVA with missing values. This is not actually possible, but we did it anyway!
Prism 8 can now analyze repeated measures data (one-, two- and three-way) by fitting a mixed effects model. The analysis works differently than ANOVA but gives the same main results when there are no missing values and gives useful results when there are missing values. Of course, the results can be interpreted only if you assume that the values are missing for random reasons.
Other improvements in repeated measures ANOVA
•Analyze three-way ANOVA with repeated measures in any or all of the three factors. Prism 7 was much more restrictive.
•Name the repeated measures factor. Earlier versions always used the name "subject". Now you can choose "litter" or "animal" or "patient" or ....
•Correct for lack of sphericity with the Geisser-Greenhouse correction. Prism 7 could already do this with one-way ANOVA. Prism 8 can do it also with two- and three-way ANOVA.

More options in regular ANOVA
•View a table of cell, row, column and grand means
When values are missing (sample sizes are unequal), Prism shows the predicted LSmeans (least square means).
•Test for homogeneity of variance by calculating the nonparametric correlation between the predicted Y values and the absolute value of the residuals.

•One-way ANOVA without assuming the data were sampled from populations with equal standard deviations. Prism will calculate the Brown-Forsythe and Welch ANOVA, followed by appropriate multiple comparisons tests: Games-Howell, Tamhane T2, DunnettT3 tests.
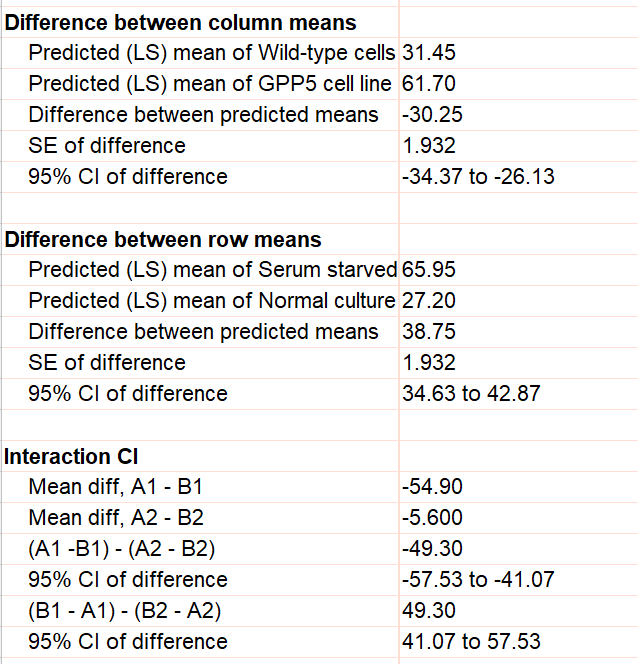
•With two-way data with only two columns and/or two rows, view the difference between the two column (or row) means along with its standard error and 95% confidence interval. If your table has two rows and two data sets, also view the interaction confidence interval.