The PC scores graph provides a visual representation of the dimension reduction achieved by PCA. After defining the PCs, the scores for each PC are calculated using the linear combinations that define each PC. As an example, the linear combinations defining PC1 and PC2 are given as follows (coefficients obtained from the eigenvectors for PC1 and PC2):
PC1 = 0.552*(Variable A) + 0.553*(Variable B) - 0.227*(Variable C) + 0.181*(Variable D) - 0.530*(Variable E)
PC2 = -0.246*(Variable A) - 0.094*(Variable B) - 0.634*(Variable C) + 0.694*(Variable D) + 0.215*(Variable E)
Entering the values of the standardized data for each variable into these formulas will generate the PC Scores table. If we then plot the PC1 and PC2 on the horizontal and vertical axis, respectively, then we will end up with the following graph, where each dot represents one row of the original data table:
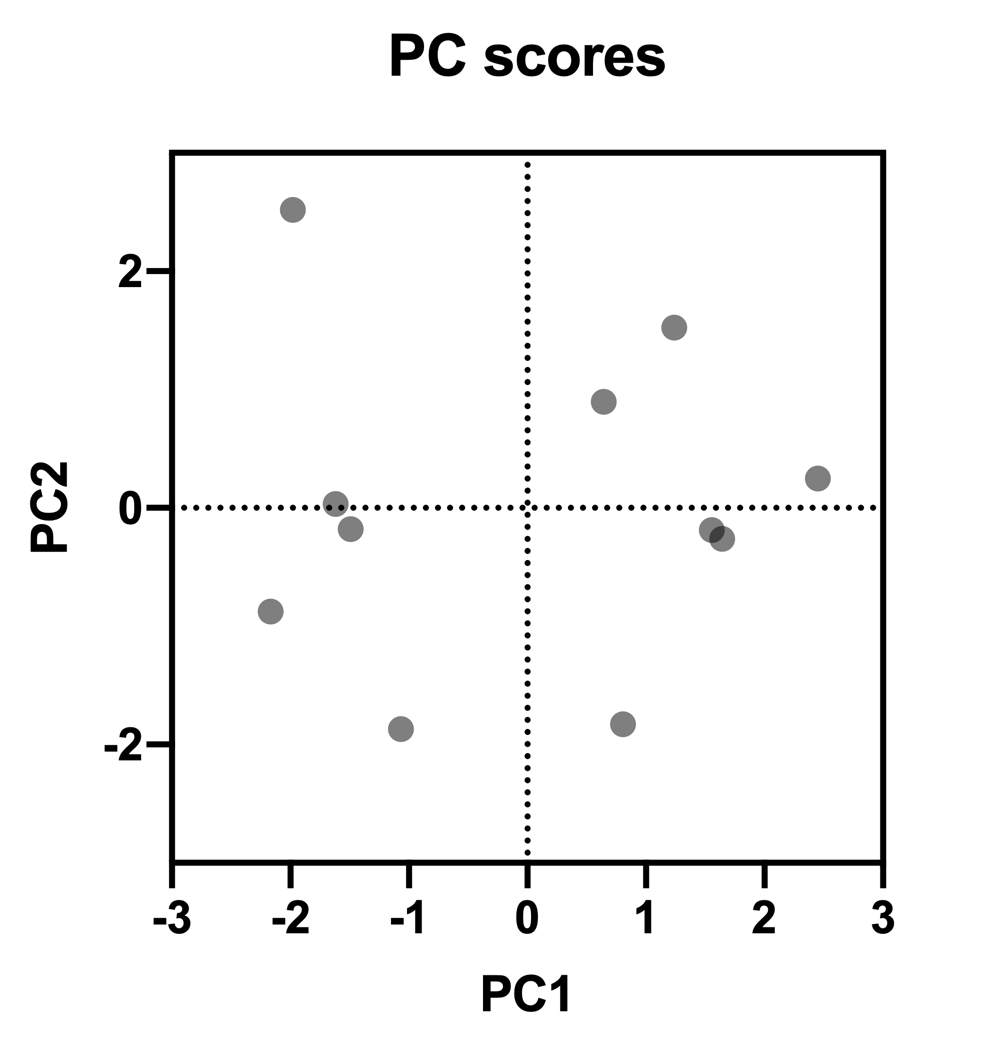
Using this type of graph, clusters of data points can often be observed. For example, in the graph above, all points on the left half of the graph correspond to rows 1-5 in the original data, while points on the right half of the graph correspond to rows 6-11 in the data.
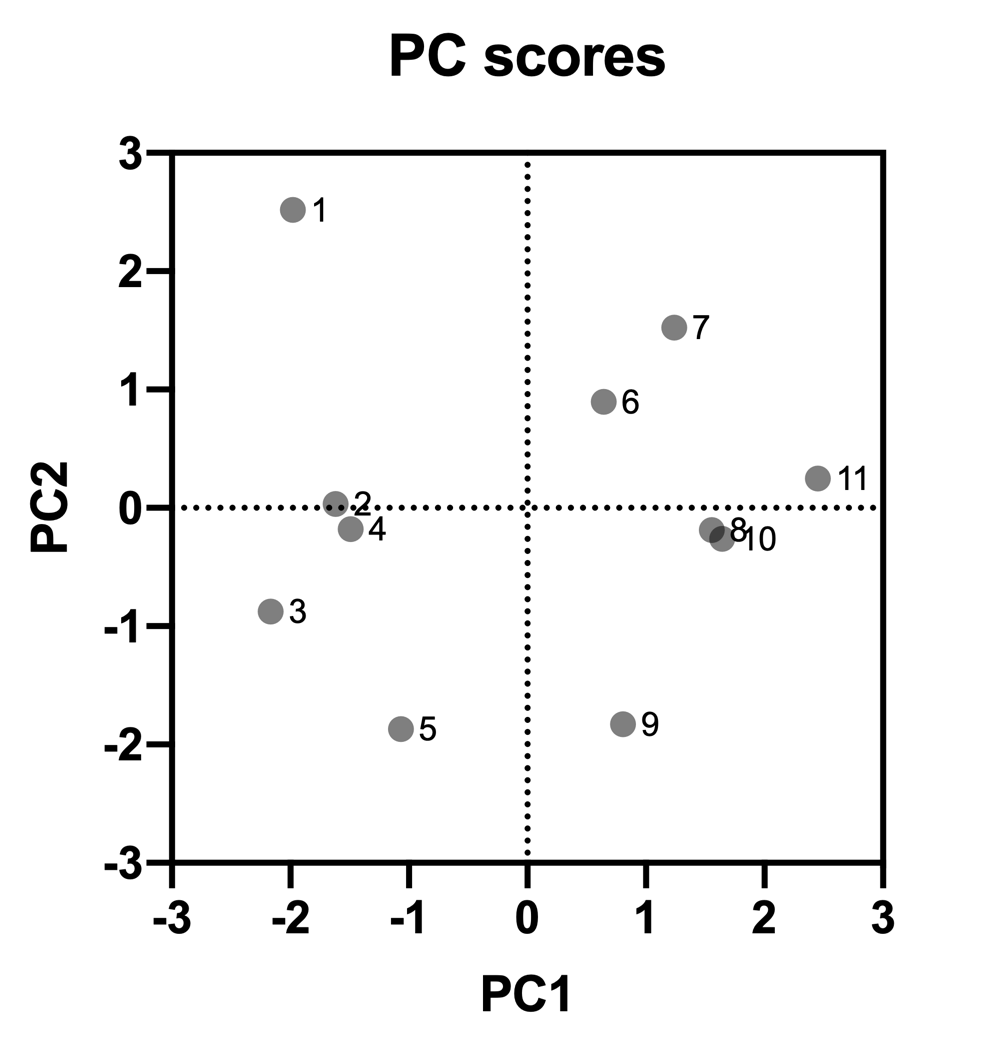
In a PCA with more than two selected components, it is sometimes useful to look at the relationship between different combinations of components (PC1 and PC3, PC2 and PC3, etc.). However, remember that the first component contains more “information” (in the form of explained variance) than the second, and the second more than the third, and so on. Thus, the most useful information is generally found on graphs comparing the first few components.