As mentioned in a previous section, loadings for a principal component represent the correlation between the variables and the principal components (if data are centered instead of standardized, the loadings represent the covariances between variables and components instead). The loadings plot visually represents these relationships.
In the loadings plot for our data, we can see that Variables A, B, and E are strongly correlated (values close to 1 or -1) with PC1, while they are only somewhat correlated with PC2. Conversely, Variables C and D correlate strongly with PC2, but are only somewhat correlated with PC1.
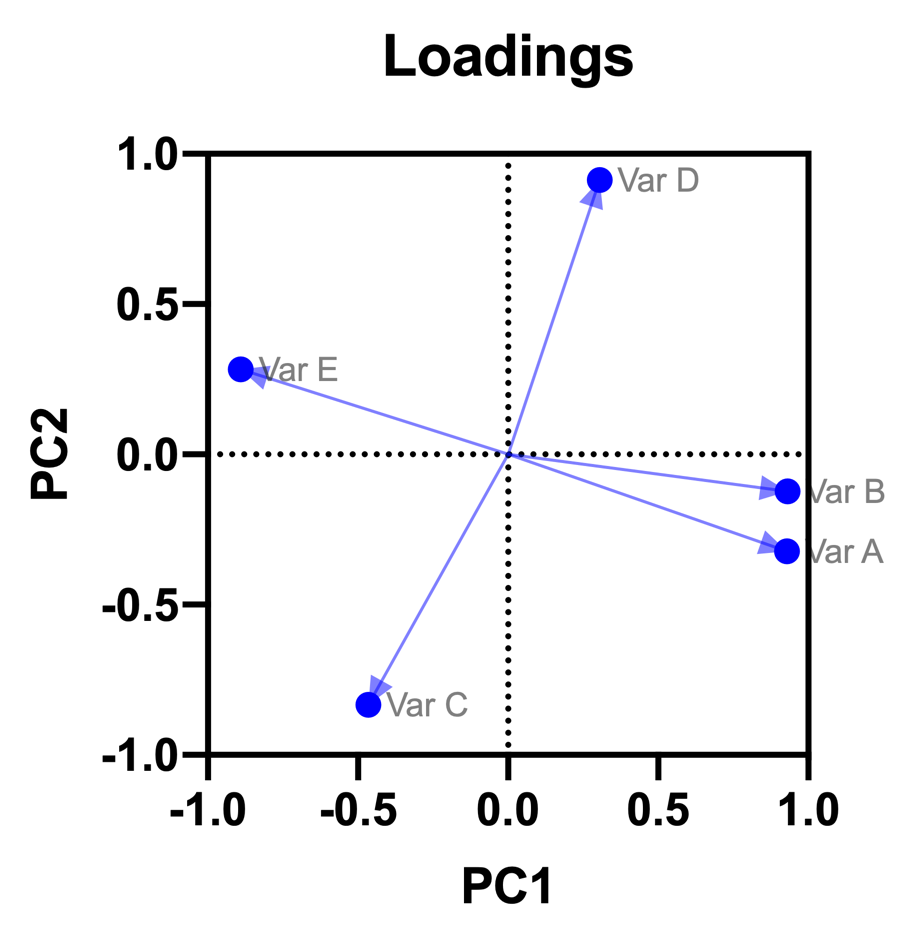
In our example, PC1 and PC2 together account for 91.18% of the cumulative proportion of variance. With so much information contained on this single graph, we can gain some insight into the relationships between individual variables. As shown on the graph above, Variables A and B are clustered closely together, indicating that these two variables are positively correlated. In comparison, the vectors for Variables A and E form a nearly 180° angle, indicating that these variables are negatively correlated. Finally, the vectors for Variables A and D form a nearly right angle, suggesting that these two variables are likely uncorrelated. Going back to our graph matrix of the original data, we can confirm that these assumptions are largely correct.