How does the QuickCalcs Post Test Calculator work?
This article describes how to perform post tests following two-way ANOVA using the Bonferroni method as detailed in pages 741-744 and 771 in J Neter, W Wasserman, and MH Kutner, Applied Linear Statistical Models , 3rd edition, Irwin, 1990.
For each comparison, the confidence interval is:
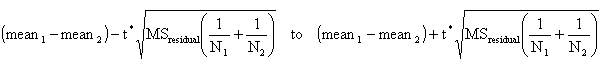
| Variable | Explanation |
|---|---|
| Mean1 | Mean of group 1, entered on the form |
| Mean2 | Mean of group 2, entered on the form |
| N1 | Sample size of group 1, entered on the form |
| N2 | Sample size of group 2, entered on the form |
| t* | This variable is defined using the Bonferroni correction for multiple comparisons. when making a single confidence interval, t* is the value of the t ratio that corresponds to a two-tailed P value of 0.05 (or whatever significance level you chose). If you are making six comparisons, t* is the t ratio that corresponds to a P value of 0.05/6, or 0.00833. the web calculator does the computation, and the formula is too complicated for hand calculation. If you want to do the calculations yourself, use Excel to compute t* using the formula =TINV(0.00833,6), which equals 3.863. the first parameter is the significance level corrected for multiple comparisons; the second is the number of degrees of freedom for the ANOVA (residuals for regular two-way ANOVA, individual for repeated measures). The value of t* will be the same for each comparison. Its value depends on the degree of confidence you desire, the number of degrees of freedom in the ANOVA, and the number of comparisons you made. |
| MSresidual | The mean square for residuals calculated by Prism or some other ANOVA program. You wouldn't want to calculate this value by hand. Some programs call this the mean square error. The value of MS residual will be the same for each comparison. |
To determine significance levels, calculate for each comparison:
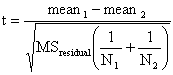
The variables are the same as used in the confidence interval calculations. But notice the key difference. Here, you calculate a t ratio for each comparison, and then use it to determine the significance level as explained in the next paragraph. When computing a confidence interval, you choose a confidence level (95% is standard) and use that to determine a fixed value from the t distribution, which we call t*. Note that the numerator is the absolute value of the difference between means, so the t ratio will always be positive.
To determine the significance level, compare the values of the t ratio computed for each comparison against the standard values, which we abbreviate t*. For example to determine whether the comparison is significant at the 5% level (P<0.05), compare the t ratios computed for each comparison to the t* value calculated for a confidence interval of 95% (equivalent to a significance level of 5%, or a P value of 0.05) corrected for the number of comparisons and taking into account the number of degrees of freedom. As shown above, this value is 3.863. If a t ratio is greater than t*, then that comparison is significant at the 5% significance level. To determine whether a comparison is significant at the stricter 1% level, calculate the t ratio corresponding to a confidence interval of 99% (P value of 0.01) with six comparisons and six degrees of freedom. First divide 0.01 by 6 (number of comparisons), which is 0.001667. Then use the Excel formula =TINV(0.001667,6) to find the critical t ratio of 5.398. Each comparison that has a t ratio greater than 5.398 is significant at the 1% level.















